Hängt eine Funktion 
vom Ortsvektor 
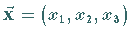ab,
,
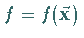dann bedingt eine infinitesimale Drehung
mit dem Winkel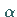 
um die Koordinatenachse 
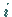eine lineare Transformation
von
nach
 |
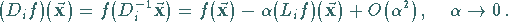(5.143) |
Wenn die neue Funktion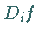 
im Punkt 
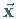denselben Wert annimmt
wie die Funktion
im Punkt 
,
dann berechnet sich die
infinitesimale Änderung mit Hilfe der Differentialoperatoren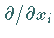 
und
 |
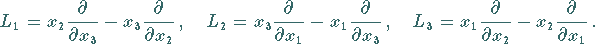(5.144) |
Hinweis: Die Operatoren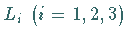 
stellen ebenfalls eine
Realisierung der infinitesimalen Generatoren der Drehgruppe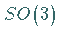 
dar.
In der Quantenmechanik entsprechen sie bis auf den Faktor 
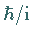den
kartesischen Komponenten des Bahndrehimpulsoperators 
:
 |
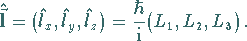(5.145) |
