Der Satz von CAYLEY beinhaltet, daß durch die
Permutationsgruppen alle Gruppen strukturell beschrieben
werden können:
Jede Gruppe ist zu einer Permutationsgruppe isomorph.
Eine zu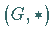 
isomorphe Permutationsgruppe 
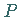ist die aus den Permutationen
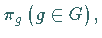die 
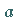auf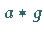 
abbilden, bestehende Untergruppe der
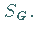Dabei ist ein zugehöriger Isomorphismus 
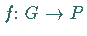durch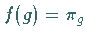 
gegeben.
