Ringhomomorphismus und Ringisomorphismus
1. Ringhomomorphismus:
Es seien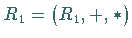 
und 
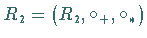Ringe.
Eine Abbildung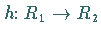 
heißt Ringhomomorphismus , wenn
für alle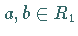 
gilt:
 |
(5.204) |
2. Kern:
Der Kern von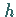 
ist die Menge aller Elemente aus 
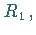die bei
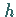auf das
neutrale Element 0 von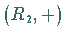 
abgebildet werden, und wird mit 
bezeichnet:
 |
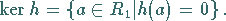(5.205) |
3. Ringisomorphismus:
Ist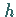
außerdem bijektiv, so heißt
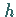Ringisomorphismus , und die
Ringe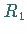 
und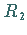 
heißen zueinander isomorph.
4. Faktorring:
Ist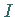 
ein Ideal eines Ringes 
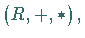so wird die Menge der Nebenklassen
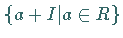von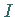
in der additiven Gruppe 
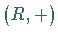des Ringes 
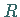bezüglich der Operationen
(s. Definition und Eigenschaften von Gruppen)
 |
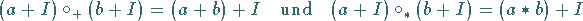(5.206) |
zu einem Ring, dem Faktorring von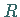
nach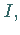 
der mit 
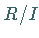bezeichnet wird.
Die Hauptideale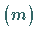 
von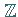 
liefern als Faktorringe gerade die Restklassenringe
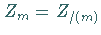
(s. Beispiele für Ringe und Körper).
