Ersetzt man im Homomorphiesatz für Gruppen den Begriff Normalteiler durch Ideal, so
erhält man den Homomorphiesatz für Ringe :
Ein Ringhomomorphismus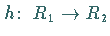
bestimmt ein Ideal von ,
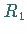nämlich
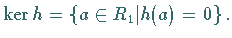Der Faktorring
ist isomorph zum homomorphen Bild
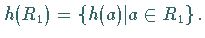Umgekehrt bestimmt jedes Ideal
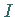von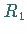
eine homomorphe Abbildung
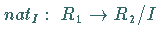mit
Diese Abbildung
wird natürlicher Homomorphismus genannt.
bestimmt ein Ideal von 
,
nämlich
Der Faktorring 
ist isomorph zum homomorphen Bild
Umgekehrt bestimmt jedes Ideal 
von 
mit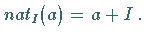 
Diese Abbildung 
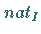wird natürlicher Homomorphismus genannt.
