Themen dieser Seite
Klassifizierung von Baryonen und Mesonen
Ersetzt man in (5.173) die Generatoren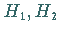 
der CARTAN-WEYL-Basis
für die LIE-Algebra 
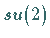durch die Operatoren
 |
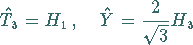(5.195) |
mit den Eigenwerten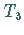 
und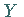 
,
wobei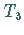
die dritte Komponente des
Isospins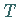 
und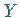 
die Hyperladung (elektrische Ladung 
)
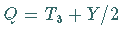bedeuten, dann
erhält man für die Gewichte (5.175) der fundamentalen Darstellung
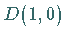von 
 |
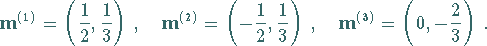(5.196) |
In der physikalischen Literatur bezeichnet man die Darstellung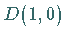
auch mit
,
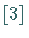weil sie ein -Multiplett mit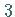 
Basiszuständen repräsentiert.
Um zu einer Klassifizierung der Hadronen ( Mesonen, Baryonen ) zu gelangen,
identifiziert man diese Zustände mit den drei Quark-Flavour-Zuständen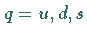 
(linke Abbildung).
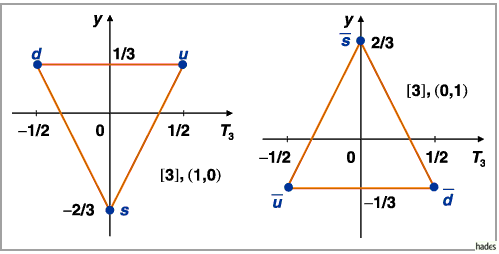
Beim Übergang zu den Antiquarks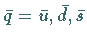 
als den
zugehörigen Antiteilchen entstehen Zustände mit entgegengesetzter Hyperladung
und entgegengesetzter 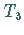-Komponente des Isospins.
Diese Zustände spannen die kontragradiente oder duale Darstellung 
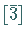(oder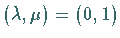 
)
der Gruppe
mit den Gewichten
 |
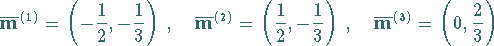(5.197) |
auf, wobei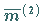 
das höchste Gewicht ist (rechte Abbildung).
(Die zu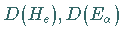 
kontragradiente oder duale Darstellung erhält man
durch den Übergang
.)
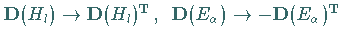SU(3) Multipletts der Baryonen
Gemäß Quarkmodell sind Baryonen aus drei Quarks zusammengesetzt.
Baryonenzustände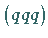 
transformieren sich als Tensoren 3. Stufe
(s. Tensoren 
ter Stufe) in den Quarkzuständen, die sich nach dem direkten
Produkt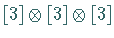 
(oder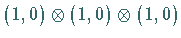 
)
der
fundamentalen Darstellung der Gruppe
transformieren.
Die Dimension des Produktraumes ist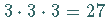 
.
Eine Ausreduktion führt auf die
CLEBSCH-GORDAN-Reihe
 |
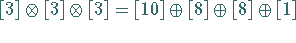(5.198) |
(oder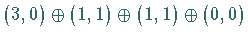 
), wobei 
(oder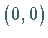 
)
die
identische Darstellung mit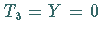 
ist.
Der Darstellungsraum zerfällt also in eine direkte Summe invarianter Unterräume
mit der Dimension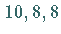 
und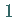 
.
Damit erhält man die folgenden -Flavour-Multipletts: ein Dekuplett, zwei
Oktetts und ein Singulett.
Die in den irreduziblen Darstellungen auftretenden Gewichte bestimmen die möglichen
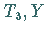-Quantenzahlen der Baryonen.
Bei einer durch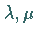 
gegebenen irreduziblen Darstellung sind die folgenden
Werte von Isospin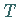
und Hyperladung
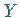möglich:
 |
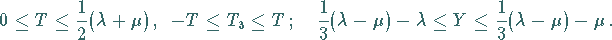(5.199) |
Für die in der Zerlegung (5.198) auftretenden Multipletts erhält man:
 |
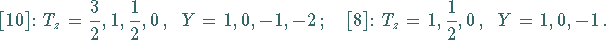(5.200) |
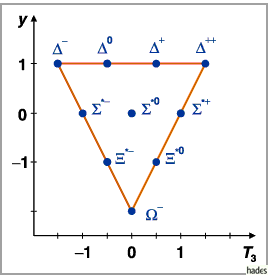
In der folgenden Abbildung ist das Dekuplett der Baryonen mit dem Spin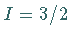 
angegeben.
Die Resonanz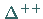 
repräsentiert den Zustand mit dem höchsten Gewicht.
Mesonen sind aus einem Quark und einem Antiquark aufgebaut.
Mesonenzustände liegen somit im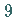 
-dimensionalen Produktraum 
;
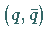sie transformieren sich gemäß der Produktdarstellung 
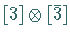(oder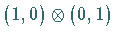 
), die nach der CLEBSCH-GORDAN-Reihe
 |
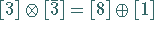(5.201) |
(oder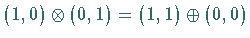 
)
zerfällt.
Die invarianten Unterräume bilden ein Oktett und ein Singulett.
Den im Oktett enthaltenen Zustand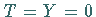 
und den Singulettzustand
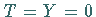faßt man in einem Gewichtsdiagramm zusammen, da die in der Natur realisierten
Zustände Mischungen der -Multiplettzustände sind.
Man erhält dann ein Nonett von Zuständen.
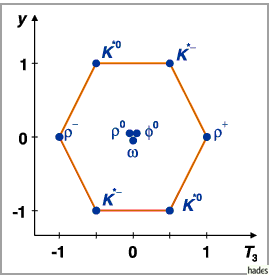
Die folgende Abbildung zeigt das Nonett der Vektormesonen mit dem Spin 
.
Das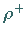 
-Meson 
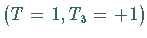repräsentiert den Zustand mit dem höchsten
Gewicht.
Es ist Teil eines Isospinmultipletts, zu dem noch das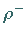 
-Meson 
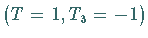und das 
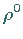-Meson 
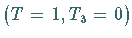gehören.
Die physikalischen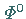 
- und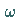 
-Mesonen sind Überlagerungen der
-Zustände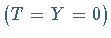 
des Oktetts 
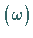und des Singuletts
.
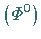