Die spezielle unitäre Gruppe 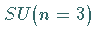 hat die Dimension
hat die Dimension 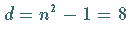 .
Die zugehörige LIE-Algebra
.
Die zugehörige LIE-Algebra 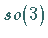 wird von
wird von 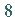 infinitesimalen Generatoren
aufgespannt, von denen beim Übergang zur CARTAN-WEYL-Basis zwei
gleichzeitig auf Diagonalform gebracht werden können:
infinitesimalen Generatoren
aufgespannt, von denen beim Übergang zur CARTAN-WEYL-Basis zwei
gleichzeitig auf Diagonalform gebracht werden können:
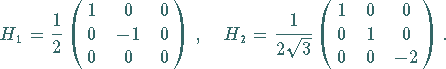 |
(5.173) |
Der Rang der LIE-Algebra 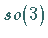 ist also
ist also 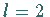 ,
so daß das
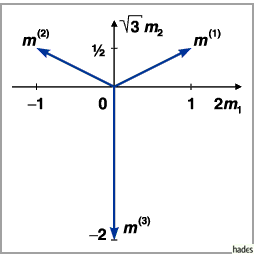
Wurzeldiagramm (s. Abbildung) und die Gewichtsdiagramme der irreduziblen
Darstellungen von
,
so daß das
Wurzeldiagramm (s. Abbildung) und die Gewichtsdiagramme der irreduziblen
Darstellungen von  Figuren in der Ebene sind.
Figuren in der Ebene sind.
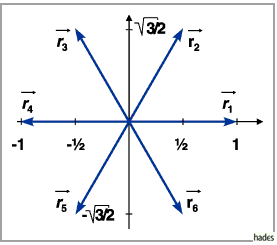
Gemäß (5.173) sind die Gewichte der fundamentalen Darstellung gegeben
durch die Vektoren
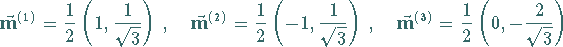 |
(5.174) |
mit 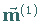 als höchstes Gewicht (s. die folgende Abbildung).
Für die sechs Wurzelvektoren findet man
als höchstes Gewicht (s. die folgende Abbildung).
Für die sechs Wurzelvektoren findet man
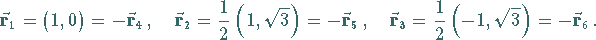 |
(5.175) |
Das höchste Gewicht jeder irreduziblen Darstellung von  kann als
Linearkombination zweier Vektoren
kann als
Linearkombination zweier Vektoren
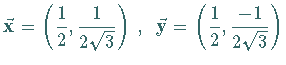 dargestellt
werden:
dargestellt
werden:
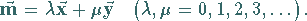 |
(5.176) |
Die ganzen Zahlen 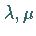 legen die Dimension der irreduziblen Darstellung
legen die Dimension der irreduziblen Darstellung
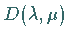 fest:
fest:
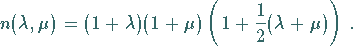 |
(5.177) |
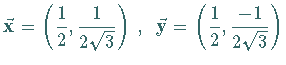 dargestellt
werden:
dargestellt
werden: