Clebsch-Gordan-Reihe
Das KRONECKER-Produkt zweier irreduzibler Darstellungen
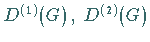 ist im allgemeinen reduzibel.
Durch eine geeignete Basistransformation im Produktraum kann
ist im allgemeinen reduzibel.
Durch eine geeignete Basistransformation im Produktraum kann
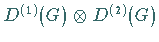 in eine direkte Summe seiner irreduziblen
Bestandteile
in eine direkte Summe seiner irreduziblen
Bestandteile 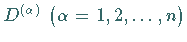 zerlegt werden
( CLEBSCH-GORDAN-Theorem ).
Diese Entwicklung nennt man CLEBSCH-GORDAN-Reihe :
zerlegt werden
( CLEBSCH-GORDAN-Theorem ).
Diese Entwicklung nennt man CLEBSCH-GORDAN-Reihe :
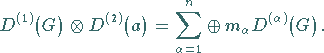 |
(5.128) |
Hier ist 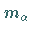 die Multiplizität, mit der die irreduzible
Darstellung
die Multiplizität, mit der die irreduzible
Darstellung 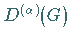 in der CLEBSCH-GORDAN-Reihe auftritt.
in der CLEBSCH-GORDAN-Reihe auftritt.
Die Matrixelemente der Basistransformation im Produktraum, die eine Reduktion des
KRONECKER-Produktes in seine irreduziblen Bestandteile bewirkt, heißen
CLEBSCH-GORDAN-KOEFFIZIENTEN .