Lineare Koordinatentransformationen, die den HAMILTON-Operator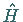 
eines quantenmechanischen Systems invariant lassen,
repräsentieren eine Symmetriegruppe 
,
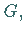deren Elemente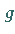 
mit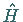
kommutieren:
 |
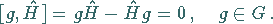(5.186) |
Die Vertauschbarkeit von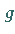
und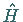
bedeutet, daß bei Anwendung des
Operatorproduktes aus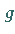
und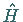
auf einen Zustand 
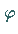die Reihenfolge
der Operatorwirkung beliebig ist:
 |
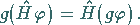(5.187) |
Folglich gilt:
Wenn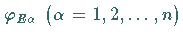 
die Eigenzustände
von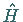
zum 
-fach entarteten Eigenwert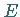 
sind, d.h.
 |
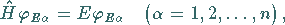(5.188) |
dann sind auch die transformierten Zustände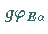 
Eigenzustände zum gleichen Eigenwert :
 |
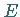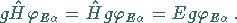(5.189) |
Die transformiert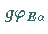en Zustände
können als
Linearkombinationen der Eigenzustände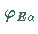 
geschrieben werden:
 |
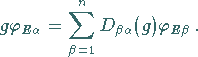(5.190) |
Die Eigenzustände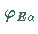
bilden demzufolge die Basis eines
-dimensionalen Darstellungsraumes für eine Darstellung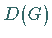 
der
Symmetriegruppe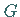 
des HAMILTON-Operatots
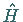mit den
Darstellungsmatrizen 
.
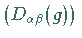Diese Darstellung ist irreduzibel, wenn keine ,,versteckten`` Symmetrien
vorliegen.
Man kann feststellen, daß sich die Energie-Eigenzustände eines
quantenmechanischen Systems durch die irreduziblen Darstellungen der
Symmetriegruppen des HAMILTON-Operators klassifizieren lassen.
Die Darstellungstheorie von Gruppen liefert damit qualitative Aussagen über
solche Strukturen des Energiespektrums eines quantenmechanischen Systems, die
allein auf seine äußeren oder inneren Symmetrien zurückgehen.
Auch die Aufspaltung entarteter Energieniveaus unter dem Einfluß einer
Störung, die die Systemsymmetrie bricht, und die Auswahlregel für die
Matrixelemente der Übergänge zwischen Energie-Eigenzuständen folgen aus
der Untersuchung der Darstellungen, nach denen sich die beteiligten Zustände
und Operatoren unter Gruppenoperationen transformieren.
Die Anwendung der Gruppentheorie in der Quantenmechanik wird ausführlich in
der Literatur dargestellt, z.B. in Lit. 5.11, 5.13, 5.21,
5.22, 5.23.
