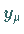|
|
|
|
gegen unabhängige Variable 
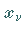austauschen lassen.
Die lineare Unabhängigkeit wird z.B. für die Rangbestimmung bei Matrizen benötigt.
Anderenfalls läßt sich die Abhängigkeitsbeziehung unmittelbar aus dem Schema
ablesen.
| Beispiel | ||||
|
| ||||
Wegen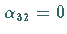 
ist kein weiterer Austausch möglich, und man kann die
Abhängigkeitsbeziehung
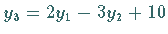ablesen.
Auch bei einer anderen Reihenfolge des Austausches wäre ein nicht austauschbares Paar
von Variablen übriggeblieben.
|
|
