Aussagen zum Rang von Matrizen
1. Matrix vom Typ A(m,n):
Da im Vektorraum der Dimension 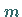 mehr als
mehr als 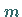 Zeilenvektoren oder Spaltenvektoren der
Dimension
Zeilenvektoren oder Spaltenvektoren der
Dimension 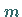 linear abhängig sind (s. lineare Unabhängigkeit), ist
der Rang
linear abhängig sind (s. lineare Unabhängigkeit), ist
der Rang 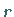 in einer Matrix
in einer Matrix  vom Typ
vom Typ 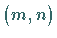 höchstens gleich der kleineren der
Zahlen
höchstens gleich der kleineren der
Zahlen 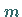 und
und 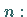
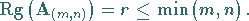 |
(4.26a) |
2. Reguläre Matrix: Eine quadratische Matrix vom Typ 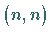 heißt eine
reguläre Matrix , wenn ihr Rang gleich
heißt eine
reguläre Matrix , wenn ihr Rang gleich 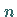 ist.
Das ist genau dann der Fall, wenn ihre Determinante
ist.
Das ist genau dann der Fall, wenn ihre Determinante 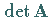 von Null
verschieden ist (s. Nullwerden einer Determinante).
Für den Rang einer regulären quadratischen Matrix
von Null
verschieden ist (s. Nullwerden einer Determinante).
Für den Rang einer regulären quadratischen Matrix  d.h.
d.h.
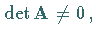 gilt
gilt
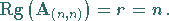 |
(4.26b) |
3. Singuläre Matrix: Eine quadratische Matrix vom Typ 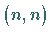 heißt eine
singuläre Matrix , wenn ihr Rang gleich
heißt eine
singuläre Matrix , wenn ihr Rang gleich 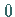 ist.
Das ist genau dann der Fall, wenn ihre Determinante
ist.
Das ist genau dann der Fall, wenn ihre Determinante 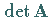 verschwindet
(s. Nullwerden einer Determinante).
Für den Rang einer singulären quadratischen Matrix
verschwindet
(s. Nullwerden einer Determinante).
Für den Rang einer singulären quadratischen Matrix 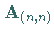 ,
d.h.
,
d.h.
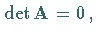 gilt
gilt
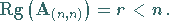 |
(4.26c) |
4. Nullmatrix: Der Rang der Nullmatrix 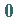 ist
ist
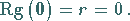 |
(4.26d) |
![]() heißt eine
reguläre Matrix , wenn ihr Rang gleich
heißt eine
reguläre Matrix , wenn ihr Rang gleich ![]() ist.
Das ist genau dann der Fall, wenn ihre Determinante
ist.
Das ist genau dann der Fall, wenn ihre Determinante ![]() von Null
verschieden ist (s. Nullwerden einer Determinante).
Für den Rang einer regulären quadratischen Matrix
von Null
verschieden ist (s. Nullwerden einer Determinante).
Für den Rang einer regulären quadratischen Matrix ![]() d.h.
d.h.
![]() gilt
gilt
![]() heißt eine
singuläre Matrix , wenn ihr Rang gleich
heißt eine
singuläre Matrix , wenn ihr Rang gleich ![]() ist.
Das ist genau dann der Fall, wenn ihre Determinante
ist.
Das ist genau dann der Fall, wenn ihre Determinante ![]() verschwindet
(s. Nullwerden einer Determinante).
Für den Rang einer singulären quadratischen Matrix
verschwindet
(s. Nullwerden einer Determinante).
Für den Rang einer singulären quadratischen Matrix ![]() ,
d.h.
,
d.h.
![]() gilt
gilt
![]() ist
ist