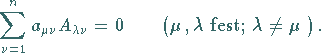Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Rechenregeln für Determinanten

Wegen des LAPLACEschen Entwicklungssatzes gelten die im folgenden für Zeilen formulierten Aussagen in gleicher Weise für Spalten.
1. Unabhängigkeit des Wertes einer Determinante: Der Wert einer Determinante ist unabhängig von der Auswahl der Entwicklungszeile.
2. Ersetzen von Adjunkten:Ersetzt man bei der Entwicklung einer Determinante nach einer ihrer Zeilen die zugehörigen Adjunkten durch die Adjunkten einer anderen Zeile, so ergibt sich Null:
(4.56)

Diese Beziehung und der Entwicklungssatz ergeben zusammengefaßt

(4.57)

Daraus erhält man für die inverse Matrix

(4.58)

wobei als adjungierte Matrix der Matrix die aus den Adjunkten der Elemente von gebildete und anschließend transponierte Matrix bezeichnet wird. Diese Matrix darf nicht mit der zu einer komplexen Matrix adjungierten Matrix (4.4) verwechselt werden.
3. Nullwerden einer Determinante:Eine Determinante ist gleich Null, wenn
a) eine Zeile aus lauter Nullen besteht oder
b) zwei Zeilen einander gleich sind oder
c) eine Zeile eine Linearkombination anderer Zeilen ist.

4. Vertauschungen und Additionen: Eine Determinante ändert ihren Wert nicht, wenn
a) in ihr die Zeilen mit den Spalten vertauscht werden. Man spricht dann von Spiegelung an der Hauptdiagonale , d.h., es gilt

(4.59)


b) zu irgendeiner Zeile eine andere Zeile addiert bzw. subtrahiert wird,
c) zu irgendeiner Zeile ein Vielfaches einer anderen Zeile addiert bzw. subtrahiert wird oder
d) zu irgendeiner Zeile eine Linearkombination anderer Zeilen addiert bzw. subtrahiert wird.

5. Vorzeichen bei Zeilenvertauschung: Bei Vertauschung zweier Zeilen ändert sich das Vorzeichen einer Determinante.
6. Multiplikation einer Determinante mit einer Zahl: Eine Determinante wird mit einer Zahl multipliziert, indem die Elemente einer einzigen Zeile mit dieser Zahl multipliziert werden. Der Unterschied gegenüber der Multiplikation einer Matrix vom Typ mit einer Zahl kommt in der Formel
(4.60)

zum Ausdruck.
7. Multiplikation zweier Determinanten:Die Multiplikation zweier Determinanten wird auf die Multiplikation ihrer Matrizen zurückgeführt:

(4.61)

Wegen (s. (4.59)) gilt

(4.62)

d.h., es können entweder Zeilen mit Spalten oder Zeilen mit Zeilen oder Spalten mit Zeilen oder Spalten mit Spalten skalar multipliziert werden.
8. Differentiation einer Determinante: Eine Determinante -ter Ordnung, deren Elemente differenzierbare Funktionen eines Parameters sind, d.h. wird nach differenziert, indem man jeweils eine Zeile differenziert und die so entstehenden Determinanten addiert.

Beispiel

Für eine Determinante vom Typ 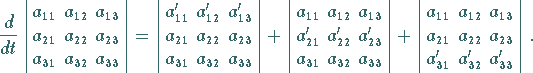erhält man: