Lineare Abhängigkeit
Es sei 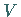 ein
ein 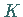 -Vektorraum.
Die Vektoren
-Vektorraum.
Die Vektoren 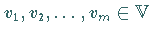 heißen linear abhängig , falls es
heißen linear abhängig , falls es
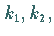
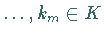 gibt, die nicht alle gleich Null sind, so daß
gibt, die nicht alle gleich Null sind, so daß
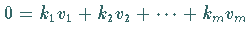 gilt, und andernfalls linear unabhängig .
Lineare Abhängigkeit von Vektoren bedeutet also, daß sich ein Vektor durch die
anderen darstellen läßt.
gilt, und andernfalls linear unabhängig .
Lineare Abhängigkeit von Vektoren bedeutet also, daß sich ein Vektor durch die
anderen darstellen läßt.
Existiert eine Maximalzahl  linear unabhängiger Vektoren in
linear unabhängiger Vektoren in  so heißt
so heißt  n-dimensional .
Diese Zahl
n-dimensional .
Diese Zahl  ist dann eindeutig bestimmt und heißt Dimension .
Je
ist dann eindeutig bestimmt und heißt Dimension .
Je  linear unabhängige Vektoren in
linear unabhängige Vektoren in 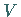 bilden eine Basis .Gibt es eine solche Maximalzahl nicht, so heißt der Vektorraum
unendlichdimensional .
Die Vektorräume aus den obigen Beispielen sind in der angegebenen Reihenfolge
bilden eine Basis .Gibt es eine solche Maximalzahl nicht, so heißt der Vektorraum
unendlichdimensional .
Die Vektorräume aus den obigen Beispielen sind in der angegebenen Reihenfolge
 -,
-, 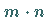 - bzw. unendlichdimensional.
- bzw. unendlichdimensional.
Aus dem Vektorraum 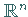 sind
sind  Vektoren genau dann linear abhängig, wenn
die Determinante der Matrix, die diese Vektoren als Spalten bzw. Zeilen enthält, gleich
0 ist.
Vektoren genau dann linear abhängig, wenn
die Determinante der Matrix, die diese Vektoren als Spalten bzw. Zeilen enthält, gleich
0 ist.
Ist 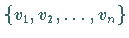 eine Basis eines
eine Basis eines  -dimensionalen
-dimensionalen 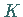 -Vektorraumes,
so besitzt jeder Vektor
-Vektorraumes,
so besitzt jeder Vektor 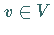 eine eindeutige Darstellung
eine eindeutige Darstellung
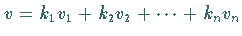 mit
mit 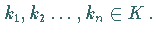
Jede Menge linear unabhängiger Vektoren eines Vektorraumes läßt sich zu einer
Basis dieses Vektorraumes ergänzen.