Hinweise zur numerischen Bestimmung von Eigenwerten
1. Die Eigenwerte könnten als Nullstellen der charakteristischen Gleichung
(4.125b) berechnet werden
(s. Beispiel A und
Beispiel B).
Dazu müssen die Koeffizienten 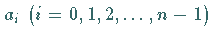 des
charakteristischen Polynoms der Matrix
des
charakteristischen Polynoms der Matrix  bestimmt werden.
Diese Vorgehensweise sollte aber vermieden werden, da sie einen außerordentlich
instabilen Algorithmus darstellt, d.h., kleine Änderungen in den Koeffizienten
bestimmt werden.
Diese Vorgehensweise sollte aber vermieden werden, da sie einen außerordentlich
instabilen Algorithmus darstellt, d.h., kleine Änderungen in den Koeffizienten 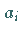 führen zu sehr großen Änderungen der Nullstellen
führen zu sehr großen Änderungen der Nullstellen 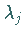 .
.
2. Für die numerische Lösung des symmetrischen Eigenwertproblems sind
zahlreiche Algorithmen entwickelt worden.
Man unterscheidet zwei Verfahrensklassen (s. Lit. 4.8):
a) Transformationsverfahren, z.B. JACOBI-Verfahren,
HOUSEHOLDER-Tridiagonalisierung, QR-Algorithmus;
b) Iterationsverfahren, z.B. Vektoriteration,
RAYLEIGH- RITZ-Algorithmus, Inverse Iteration, LANCZOS-Verfahren,
Bisektionsverfahren.
Als Beispiel wird die Potenzmethode von MISES betrachtet.
Potenzmethode von Mises
Hierbei handelt es
sich um ein Iterationsverfahren zur Bestimmung des betragsgrößten
Eigenwertes und des zugehörigen Eigenvektors einer Matrix
 ,
falls
,
falls  reell und symmetrisch ist und einen
betragsgrößten (dominanten) Eigenwert hat.
Dieser sei
reell und symmetrisch ist und einen
betragsgrößten (dominanten) Eigenwert hat.
Dieser sei 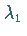 .
Dann gilt:
.
Dann gilt:
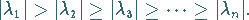 |
(4.143) |
Die Matrix  hat
hat 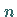 linear unabhängige Eigenvektoren
linear unabhängige Eigenvektoren
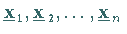 .
Daraus folgt:
.
Daraus folgt:
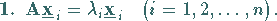 |
(4.144) |
2. Jedes Element 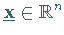 läßt sich als
Linearkombination der Eigenvektoren
läßt sich als
Linearkombination der Eigenvektoren 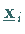 darstellen:
darstellen:
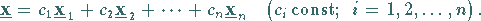 |
(4.145) |
Multipliziert man (4.145) mit  und berücksichtigt (4.144),
dann erhält man nach
und berücksichtigt (4.144),
dann erhält man nach 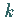 -maliger Multiplikation:
-maliger Multiplikation:
Daraus folgt wegen (4.143):
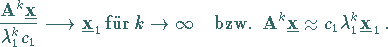 |
(4.147) |
Die Aussagen (4.147) sind Grundlage des folgenden Iterationsverfahrens:
Schritt 1:
Wahl eines beliebigen Startvektors 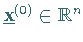 .
.
Schritt 2:
Iterative Berechnung von 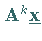 gemäß
gemäß
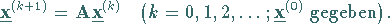 |
(4.148) |
Daraus folgt unter Beachtung von (4.146):
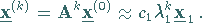 |
(4.149) |
Schritt 3:
Aus (4.148) und (4.149) folgt:
d.h. für große Werte von 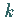 unterscheiden sich aufeinanderfolgende
Näherungsvektoren
unterscheiden sich aufeinanderfolgende
Näherungsvektoren 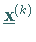 durch den Faktor
durch den Faktor 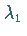 .
.
Schritt 4:
Aus (4.149) und (4.150) erhält man zur Berechnung von
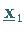 und
und 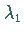 :
:
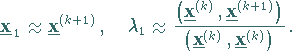 |
(4.151) |
Hinweise:
1. Da Eigenvektoren nur bis auf einen Zahlenfaktor eindeutig bestimmt sind,
ist es numerisch zweckmäßig, die Vektoren 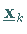 zu normieren, z.B. in der im Beispiel angegebenen Weise.
zu normieren, z.B. in der im Beispiel angegebenen Weise.
2. Der betragskleinste Eigenwert von 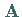 und der zugehörige
Eigenvektor lassen sich bestimmen, indem man die Potenzmethode auf die Inverse
und der zugehörige
Eigenvektor lassen sich bestimmen, indem man die Potenzmethode auf die Inverse
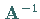 von
von 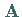 anwendet.
anwendet.
3. Zur Bestimmung der übrigen Eigenwerte und Eigenvektoren von 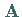 kann die Potenzmethode ebenfalls angewendet werden.
Ist der Eigenvektor
kann die Potenzmethode ebenfalls angewendet werden.
Ist der Eigenvektor 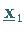 bekannt, dann wird zur Bestimmung von
bekannt, dann wird zur Bestimmung von
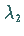 ein Startvektor gewählt, der zu
ein Startvektor gewählt, der zu 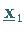 orthogonal
ist, und dann wie bei der Bestimmung von
orthogonal
ist, und dann wie bei der Bestimmung von 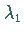 verfahren,
falls
verfahren,
falls 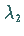 dominant gegenüber
dominant gegenüber 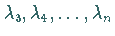 ist.
Zur Bestimmung von
ist.
Zur Bestimmung von 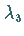 wird dann ein Startvektor gewählt, der orthogonal
zu
wird dann ein Startvektor gewählt, der orthogonal
zu 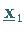 und
und 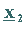 ist, usw.
Diese Vorgehensweise wird auch als Deflation bezeichnet.
ist, usw.
Diese Vorgehensweise wird auch als Deflation bezeichnet.
4. Aufgrund der Iterationsvorschrift (4.148) wird
die Potenzmethode auch Vektoriteration genannt.
![]() zu normieren, z.B. in der im Beispiel angegebenen Weise.
zu normieren, z.B. in der im Beispiel angegebenen Weise.
![]() und der zugehörige
Eigenvektor lassen sich bestimmen, indem man die Potenzmethode auf die Inverse
und der zugehörige
Eigenvektor lassen sich bestimmen, indem man die Potenzmethode auf die Inverse
![]() von
von ![]() anwendet.
anwendet.
![]() kann die Potenzmethode ebenfalls angewendet werden.
Ist der Eigenvektor
kann die Potenzmethode ebenfalls angewendet werden.
Ist der Eigenvektor ![]() bekannt, dann wird zur Bestimmung von
bekannt, dann wird zur Bestimmung von
![]() ein Startvektor gewählt, der zu
ein Startvektor gewählt, der zu ![]() orthogonal
ist, und dann wie bei der Bestimmung von
orthogonal
ist, und dann wie bei der Bestimmung von ![]() verfahren,
falls
verfahren,
falls ![]() dominant gegenüber
dominant gegenüber ![]() ist.
Zur Bestimmung von
ist.
Zur Bestimmung von ![]() wird dann ein Startvektor gewählt, der orthogonal
zu
wird dann ein Startvektor gewählt, der orthogonal
zu ![]() und
und ![]() ist, usw.
Diese Vorgehensweise wird auch als Deflation bezeichnet.
ist, usw.
Diese Vorgehensweise wird auch als Deflation bezeichnet.