|
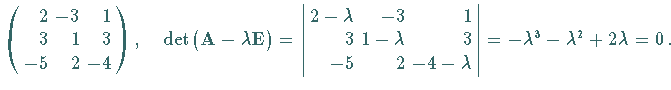
Die Eigenwerte sind 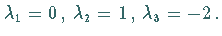
Die Eigenvektoren werden aus den zugehörigen homogenen linearen Gleichungssystemen
bestimmt.
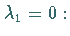
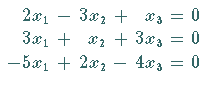
Man erhält z.B. nach dem Austauschverfahren 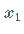 beliebig,
beliebig,
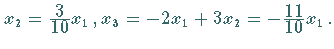 Man wählt
Man wählt 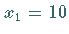 und erhält den Eigenvektor
und erhält den Eigenvektor
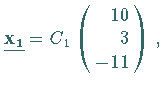 wobei
wobei 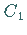 eine beliebige Konstante ist.
eine beliebige Konstante ist.
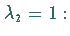 Das zugehörige homogene System ergibt
Das zugehörige homogene System ergibt 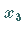 beliebig,
beliebig,
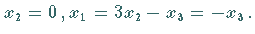 Man wählt
Man wählt 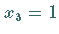 und erhält den Eigenvektor
und erhält den Eigenvektor
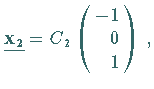 wobei
wobei 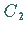 eine beliebige Konstante ist.
eine beliebige Konstante ist.
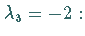 Das zugehörige homogene System ergibt
Das zugehörige homogene System ergibt 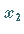 beliebig,
beliebig,
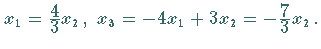 Man wählt
Man wählt 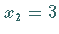 und erhält den Eigenvektor
und erhält den Eigenvektor
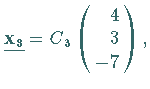 wobei
wobei 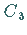 eine beliebige Konstante ist.
eine beliebige Konstante ist.
|