Der Vektor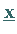 
ist genau dann eine Lösung von (4.119), wenn der
Restvektor 
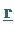orthogonal zu allen Spalten von 
ist.
Das bedeutet:
 |
(4.120) |
Diese Gleichung stellt ein lineares Gleichungssystem mit quadratischer Koeffizientenmatrix
dar.
Es wird als System der Normalgleichungen bezeichnet.
Seine Dimension ist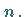 
Den Übergang von (4.117) zu (4.120) nennt man
GAUSS-Transformation .
Die Matrix 
ist symmetrisch.
Hat die Matrix
den Rang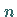 
(wegen 
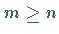spricht man in diesem
Falle von Vollrang ), dann ist die Matrix
positiv definit
und insbesondere regulär, d.h., das System der Normalgleichungen hat bei Vollrang von
eine eindeutige Lösung.
