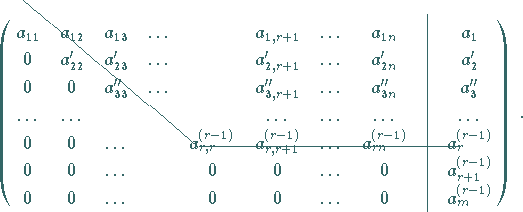Der erste GAUSS-Schritt wird an der
erweiterten Koeffizientenmatrix 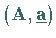 demonstriert:
demonstriert:
Es sei 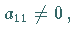 wenn nicht, dann werden entsprechende Gleichungen vertauscht.
In der Matrix
wenn nicht, dann werden entsprechende Gleichungen vertauscht.
In der Matrix
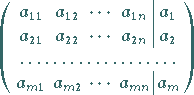 |
(4.115a) |
werden die Glieder der 1. Zeile der Reihe nach mit
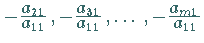 multipliziert und die Ergebnisse zur 2., 3.,...,
multipliziert und die Ergebnisse zur 2., 3.,...,
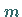 -ten Zeile addiert.
Die umgeformte Matrix hat dann die Form
-ten Zeile addiert.
Die umgeformte Matrix hat dann die Form
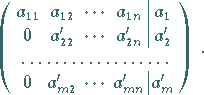 |
(4.115b) |
Die 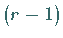 -malige Anwendung dieses GAUSS-Schrittes liefert
-malige Anwendung dieses GAUSS-Schrittes liefert
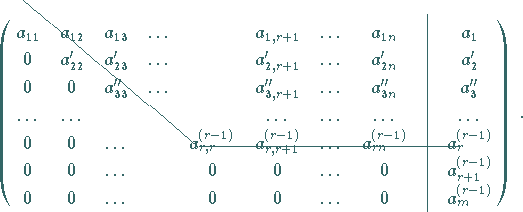 | (4.116) |
|
GAUSS-Schritte sind elementare Umformungen, durch die der Rang der Matrix
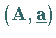 und damit auch die Lösung und das Lösungsverhalten
des Systems nicht geändert werden.
und damit auch die Lösung und das Lösungsverhalten
des Systems nicht geändert werden.
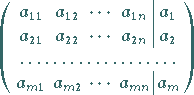
![]() multipliziert und die Ergebnisse zur 2., 3.,...,
multipliziert und die Ergebnisse zur 2., 3.,...,
![]() -ten Zeile addiert.
Die umgeformte Matrix hat dann die Form
-ten Zeile addiert.
Die umgeformte Matrix hat dann die Form
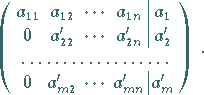
![]() -malige Anwendung dieses GAUSS-Schrittes liefert
-malige Anwendung dieses GAUSS-Schrittes liefert