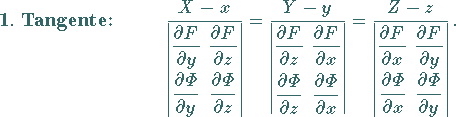Gleichungen der Elemente des begleitenden Dreibeins

(3.492)

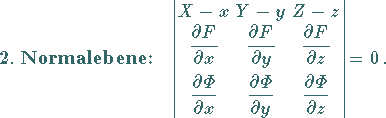(3.493)

Dabei sind die Koordinaten des Kurvenpunktes und die laufenden Koordinaten der Tangente bzw. der Normalebene; die partiellen Ableitungen beziehen sich auf den Punkt .

Tabelle Vektor- und Koordinatengleichungen von Raumkurvengrößen

Vektorgleichung	Koordinatengleichung
Tangente:
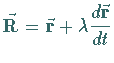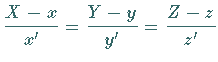Normalebene:
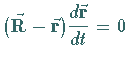Schmiegungsebene:
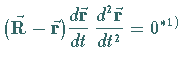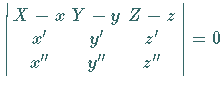Binormale:
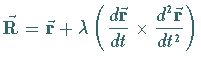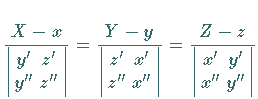rektifizierende Ebene:
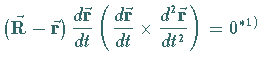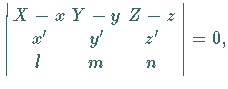
	wo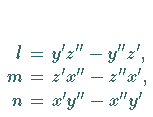
Hauptnormale:
-Ortsvektor der Raumkurve,     -Ortsvektor der Raumkurvengröße
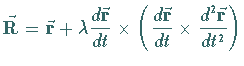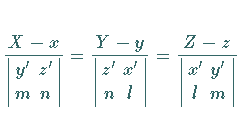*1) s. Spatprodukt dreier Vektoren.

Definition der Kurve als Funktion eines Parameters t in der Parameterform und als Vektorgleichung: Die Definition der Kurve als Funktion eines Parameters in der Parameterform und als Vektorgleichung erfolgt gemäß (3.487) und wobei (3.489).
Die Vektor- und Koordinatengleichungen von Raumkurvengrößen des Punktes mit sowie sind in der folgenden Tabelle zusammengefaßt. Dabei sind und die laufenden Koordinaten und der Radiusvektor eines Dreibeinelements. Die Ableitungen nach dem Parameter beziehen sich auf den Punkt .
Definition der Kurve als Funktion der Bogenlänge s in der Parameterform und als Vektorgleichung: Die Definition der Kurve als Funktion der Bogenlänge in der Parameterform und als Vektorgleichung erfolgt gemäß (3.488a) und wobei (3.490).
Wenn als Parameter die Bogenlänge gewählt wird, dann gelten für die Tangente und die Binormale sowie für die Normal- und Schmiegungsebene dieselben Gleichungen wie im Falle des vorhergehenden Abschnittes; es ist lediglich durch zu ersetzen. Die Gleichungen der Hauptnormalen und der rektifizierenden Ebene werden einfacher, wie aus der folgenden Tabelle zu ersehen ist.

Tabelle Vektor- und Koordinatengleichungen von
Raumkurvengrößen als Funktion von der Bogenlänge

Element des Dreibeins	Vektorgleichung	Koordinatengleichung
Hauptnormale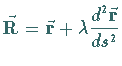
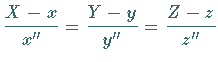Rektifizierende Ebene
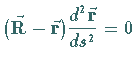-Ortsvektor der Raumkurve,     -Ortsvektor der Raumkurvengröße