Für die gewöhnlichen Kurvenpunkte liegt die Raumkurve in der Umgebung des Punktes
auf einer Seite der Rektifizierungsebene und schneidet sowohl die Normal- als auch
die Schmiegungsebene (linke Abbildung).
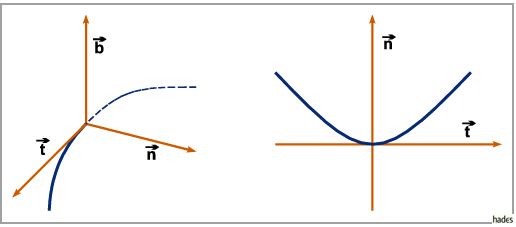
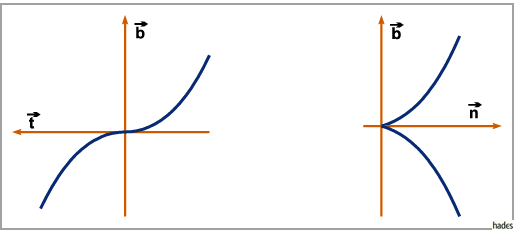
Die Projektionen eines kleinen Kurvenabschnitts um den Punkt
auf die drei Ebenen
haben dabei näherungsweise die folgende Gestalt:
1. Quadratische Parabel auf die Schmiegungsebene (zweite Abbildung);
2. kubische Parabel auf die Rektifizierungsebene (dritte Abbildung);
3. semikubische Parabel auf die Normalebene (vierte Abbildung).
Wenn die Krümmung oder die Windung der Kurve im Punkt
gleich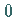 
sind oder
wenn
ein singulärer Punkt ist, also wenn 
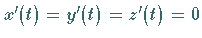ist,
dann kann die Kurve auch eine andere Gestalt haben
(s. Lit. 22.2, Band 2, Teil 7).
