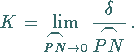|
|
|
|
einer Kurve im Punkt 
ist der Grenzwert des Verhältnisses
des Winkels 
zwischen den positiven Tangentenrichtungen in den Punkten
und 
zur Bogenlänge 
für 
 |
(3.458) |
gibt an, ob die Kurve mit ihrer konkaven Seite
nach der positiven 
oder negativen 
Seite der Kurvennormalen
zeigt (s. Kurvennormale).
Anders ausgedrückt liegt der Krümmungsmittelpunkt für 
auf der
positiven Seite der Kurvennormalen, für 
auf der negativen.
Manchmal wird die Krümmung
prinzipiell als positive Größe aufgefaßt.
Dann ist immer der Absolutbetrag des Grenzwertes zu nehmen.
einer Kurve im Punkt
ist der reziproke Wert des Betrags der Krümmung:
 |
(3.459) |
ist in einem Punkt
um so größer, je kleiner der
Krümmungskreisradius
ist.
| Beispiel A | |
|
Für einen Kreis mit dem Radius | |
| Beispiel B | |
|
Für die Gerade ist | |
Formeln für Krümmung und Krümmungskreisradius
Mit 
und 
gilt allgemein
 |
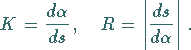(3.460) |
und 
 |
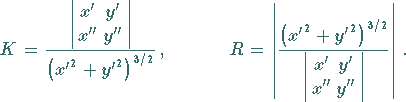(3.462) |
 |
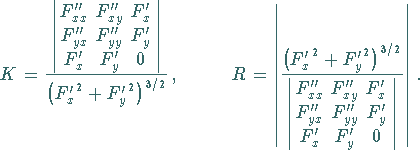(3.463) |
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
| Beispiel C | |
|
| |
| Beispiel D | |
|
| |
|
|
sind Krümmung
und Krümmungskreisradius 
für alle Punkte konstant.
und 
