Krümmungskreis und Krümmungskreismittelpunkt
1. Krümmungskreis: Der Krümmungskreis im Punkt 
wird die Grenzlage
eines Kreises genannt, der durch
und zwei benachbarte Punkte 
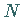und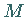 
der
Kurve geht, wenn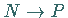 
und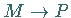 
gehen.
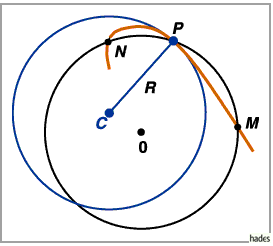
Er verläuft durch den betreffenden Kurvenpunkt und hat dort dieselbe 1. und
2. Ableitung wie die Kurve.
Demgemäß schmiegt er sich der Kurve im Berührungspunkt besonders gut an.
Er wird Schmiegkreis oder Krümmungskreis genannt.
Sein Radius heißt Krümmungskreisradius .
Es zeigt sich, daß er der Kehrwert des Absolutbetrages der Kurvenkrümmung ist.
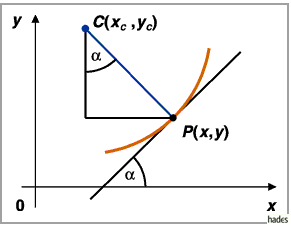
2. Krümmungskreismittelpunkt: Der Mittelpunkt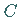 
des Krümmungskreises
ist der Krümmungsmittelpunkt des Punktes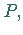 
.
Er liegt auf der konkaven Seite der Kurve und auf der zugehörigen Kurvennormalen.
3. Koordinaten des Krümmungskreismittelpunktes Die Berechnung der
Koordinat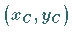en 
des Krümmungskreismittelpunktes kann je nach der
Definitionsform der Kurvengleichung mit Hilfe der folgenden Formeln
erfolgen.
Definition gemäß (3.448):
 |
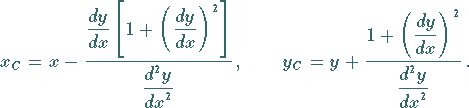(3.465) |
Definition gemäß (3.449):
 |
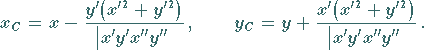(3.466) |
Definition gemäß (3.450):
 |
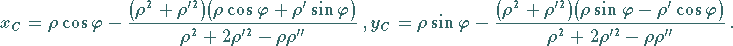(3.467) |
Definition gemäß (3.447):
 |
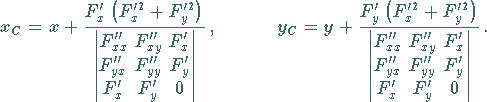(3.468) |
Diese Formeln können auch in der Form
hingeschrieben werden, wobei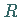 
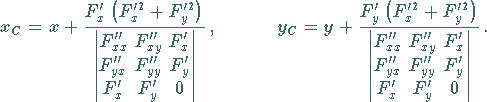
gemäß (3.461) bis
(3.464) berechnet wird.
