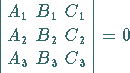Themen dieser Seite
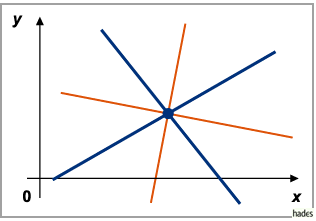
Schnittpunkt von Geraden
Um die Koordinaten 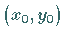 des Schnittpunktes zweier Geraden zu berechnen,
ist die Lösung des aus ihren Gleichungen zu bildenden Gleichungssystems zu berechnen.
Wenn die Geraden durch die Gleichungen
des Schnittpunktes zweier Geraden zu berechnen,
ist die Lösung des aus ihren Gleichungen zu bildenden Gleichungssystems zu berechnen.
Wenn die Geraden durch die Gleichungen
 |
(3.330a) |
gegeben sind, dann gilt
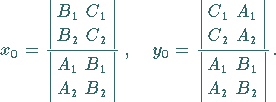 |
(3.330b) |
Wenn 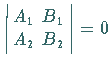 ist, dann sind die Geraden parallel.
Ist
ist, dann sind die Geraden parallel.
Ist 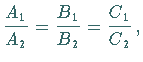 dann fallen die Geraden
zusammen.
dann fallen die Geraden
zusammen.
Geradenbüschel:
Wenn eine dritte Gerade mit der Gleichung
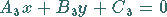 |
(3.331a) |
durch den Schnittpunkt der ersten beiden Geraden gehen soll, dann muß die Bedingung
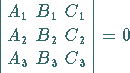 |
(3.331b) |
erfüllt sein.
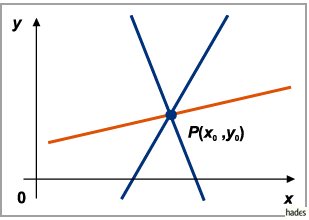
Die Gleichung
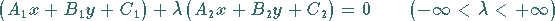 |
(3.331c) |
beschreibt alle Geraden die durch den Schnittpunkt 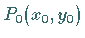 der beiden Geraden
(3.330a) hindurchgehen.
Durch (3.331c) wird ein Geradenbüschel mit dem Träger
der beiden Geraden
(3.330a) hindurchgehen.
Durch (3.331c) wird ein Geradenbüschel mit dem Träger 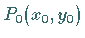 definiert.
Wenn die Gleichungen der ersten beiden Geraden in Normalform gegeben sind, dann erhält
man für
definiert.
Wenn die Gleichungen der ersten beiden Geraden in Normalform gegeben sind, dann erhält
man für 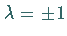 die Gleichungen der Winkelhalbierenden der von den beiden
Geraden eingeschlossenen Winkel.
die Gleichungen der Winkelhalbierenden der von den beiden
Geraden eingeschlossenen Winkel.
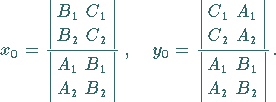
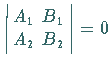 ist, dann sind die Geraden parallel.
Ist
ist, dann sind die Geraden parallel.
Ist 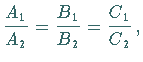 dann fallen die Geraden
zusammen.
dann fallen die Geraden
zusammen.