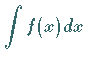|
|
|
|
versucht Mathematica, das unbestimmte
Integral 
zu bestimmen.
Wenn das Integral Mathematica bekannt ist, gibt es dieses ohne die
Integrationskonstante wieder.
Mathematica nimmt an, daß jeder Ausdruck, der die Integrationsvariable nicht
enthält, auch nicht von dieser abhängt.
Den bei der Integration (s. Integrationsregeln) auftretenden Problemen kann
Mathematica nicht ausweichen.
Im allgemeinen findet es unbestimmte Integrale, wenn sich diese durch elementare Funktionen,
wie rationale Funktionen, Exponential- und Logarithmusfunktionen sowie den
trigonometrischen und deren inversen Funktionen ausdrücken lassen.
Wenn Mathematica nicht in der Lage ist, das Integral zu bestimmen, gibt es die
Eingabe zurück.
Allerdings kennt Mathematica einige spezielle Funktionen, die durch nicht elementar
bestimmbare Integrale definiert sind, wie z.B. die elliptischen Funktionen und andere.
Zur Demonstration der Möglichkeiten von Mathematica werden einige Beispiele betrachtet, die im Unterkapitel Unbestimmte Integrale behandelt werden.
| Beispiel A | |
|
| |
 |
 |
 |
|
 |
|
 |
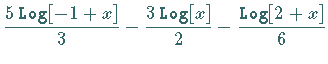| Beispiel B | |
|
| |
 |
|
 |
|
 |
|
 |
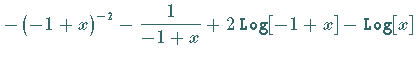(20.69) |
| Beispiel A | |
|
Es wird das Beispiel A mit dem Integral 
| |
 |
|
 |
|
 |
|
 |
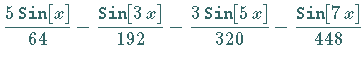| Beispiel B | |
|
Es wird das Beispiel B mit dem Integral 
| |
 |
|
 |
|
 |
|
 |
| Beispiel | |
|
| |
|
|