Berechnung von Differentialquotienten

Themen dieser Seite

Berechnung von Differentialquotienten

Operator der Differentiation

Der Differentiationsoperator wurde als

eingeführt. Seine vollständige Schreibweise lautet

(20.68)

Die Argumente geben an, wie oft nach der jeweiligen Variablen differenziert werden soll. In diesem Sinne handelt es sich um einen Operator der partiellen Differentiation. Mathematica versucht die Darstellung des Ergebnisses als reine Funktion.

Differentiation von Funktionen

Die Differentiation einer vorgegebenen Funktion kann vereinfachend durch den Operator

durchgeführt werden. Mit

wird die Ableitung der Funktion

angegeben.

gehört zu einer Gruppe von Differentialoperationen, die in der folgenden Tabelle aufgeführt sind.

Tabelle Operationen der Differentiation

liefert die -te Ableitung der Funktion . Entsprechend liefern:

mehrfache Ableitungen jeweils -mal nach

das vollständige Differential der Funktion

die vollständige Ableitung der Funktion

die vollständige Ableitung einer Funktion mehrerer Veränderlicher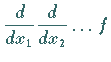

Für die beiden Beispiele aus Abschnitt Grundregeln für das Differenzieren erhält man:

Beispiel A

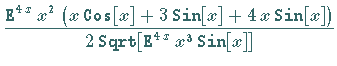Beispiel B

Die Anweisung

liefert die vollständige Ableitung bzw. das vollständige Differential.

Beispiel C

Beispiel D

Mathematica nimmt in diesen letzten Beispielen an, daß eine Funktion von ist, die es jedoch nicht kennt, und schreibt den zweiten Teil der Ableitung deshalb wieder symbolisch.

Wenn Mathematica bei der Differentiation auf eine symbolische Funktion stößt, beläßt es diese in der allgemeinen Form und drückt die Ableitung in der Form aus.

Beispiel E

Mathematica kennt die Regeln für die Differentiation von Produkten, Quotienten und die Kettenregel und kann diese auch formal anwenden:

Beispiel F

Beispiel G

	liefert die -te Ableitung der Funktion . Entsprechend liefern:
	mehrfache Ableitungen jeweils -mal nach
	das vollständige Differential der Funktion
	die vollständige Ableitung der Funktion
	die vollständige Ableitung einer Funktion mehrerer Veränderlicher

Beispiel D
	Mathematica nimmt in diesen letzten Beispielen an, daß eine Funktion von ist, die es jedoch nicht kennt, und schreibt den zweiten Teil der Ableitung deshalb wieder symbolisch.