Lösung linearer Gleichungssysteme

(20.67)

Besitzt das System keine Lösung, dann wird die Null-Sequenz zurückgegeben. Hat das System mehrere linear unabhängige Lösungen, so werden diese in Parameterdarstellung wiedergegeben.

Die Operation findet eine Basis im Nullraum der Matrix , der für eine singuläre Matrix von Null verschieden ist.

Für die Lösung von Gleichungssystemen können auch die Operationen der Matrixmultiplikation und die Bestimmung von inversen Matrizen benutzt werden.

Beispiel A

Es wird das Beispiel aus Abschnitt Triviale Lösung und Fundamentalsystem des homogenen Systems 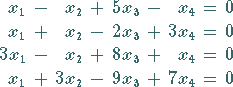betrachtet, dessen Matrix singulär ist. Das dort untersuchte homogene System besitzt nichttriviale Lösungen. Zur Lösung wird zunächst die Matrix definiert: Mit kann man sich überzeugen, daß sie singulär ist, und über kann die Liste zweier linear unabhängiger Vektoren bestimmt werden. Diese Vektoren bilden eine Basis im zweidimensionalen Nullraum der Matrix .

Für den allgemeinen Fall stellt Maple Operationen zur Anwendung des GAUSSschen Algorithmus zur Verfügung, die in der folgenden Tabelle aufgeführt sind.

Tabelle Operationen des GAUSSschen Algorithmus

	erzeugt aus durch Addition von Vielfachen der -ten Zeile zu allen anderen Zeilen eine Matrix, deren -te Spalte außer aus Nullen besteht
	erzeugt die durch Zeilenpivotisierung entstehende GAUSSsche Dreiecksmatrix. Die Matrixelemente müssen rationale Zahlen sein
	erzeugt eine Diagonalmatrix nach dem GAUSS-JORDAN-Verfahren, die Matrixelemente können Gleitpunktzahlen sein
	erzeugt die Matrix, die durch Anfügen einer Spalte (gegeben durch den Vektor ) aus entsteht

Beispiel B
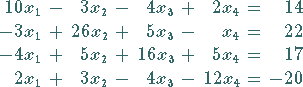
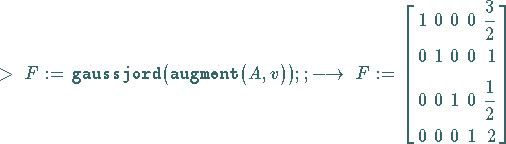
	Es soll das System aus Kapitel Numerische Mathematik, Abschnitt GAUSS-SEIDEL-Verfahren gelöst werden. Hier ist Mit linsolve erhält man Der GAUSS-Algorithmus wird mit angewendet.

Beispiel C

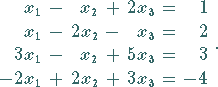
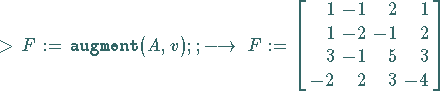
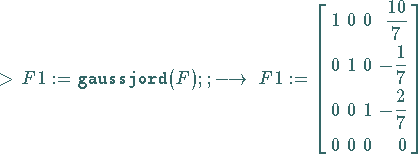
Es soll das inhomogene Gleichungssystem des Beispiels B aus Abschnitt Allgemeine Regel für das inhomogene System gelöst werden. Dazu werden zunächst die zugehörige Matrix und der Vektor der rechten Seite definiert: Das System ist überbestimmt. Um es zu lösen, kann linsolve nicht benutzt werden. Daher bestimmt man Mit gaussjord kann die Matrix in eine obere Dreiecksform gebracht werden: Der Lösungsvektor ist unmittelbar aus ablesbar.