Verallgemeinerte Gaußsche Glockenkurve
Die Kurve der Funktion
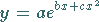 |
(2.61) |
kann als Verallgemeinerung der GAUSSschen Glockenkurve 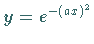 (2.58) aufgefaßt werden; sie stellt eine symmetrische Kurve zur vertikalen
Geraden
(2.58) aufgefaßt werden; sie stellt eine symmetrische Kurve zur vertikalen
Geraden 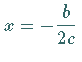 dar, wobei die
dar, wobei die  -Achse nicht geschnitten wird
und der Schnittpunkt
-Achse nicht geschnitten wird
und der Schnittpunkt  mit der
mit der 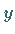 -Achse bei
-Achse bei 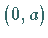 liegt.
liegt.
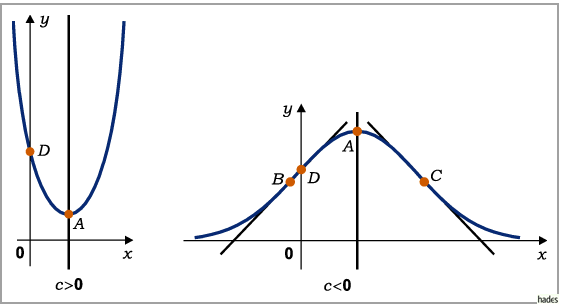
Der Verlauf der Funktion hängt von den Vorzeichen von  und
und 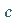 ab.
Hier wird nur der Fall
ab.
Hier wird nur der Fall 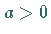 betrachtet, da die Kurve zu
betrachtet, da die Kurve zu 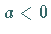 durch Spiegelung
an der
durch Spiegelung
an der  -Achse erhalten werden kann.
-Achse erhalten werden kann.
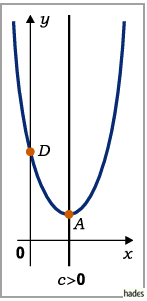
Fall
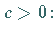 Die Funktion nimmt von
Die Funktion nimmt von 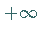 bis zum Minimum ab, um dann wieder bis
bis zum Minimum ab, um dann wieder bis 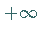 anzuwachsen. Dabei bleibt sie stets positiv.
Das Minimum
anzuwachsen. Dabei bleibt sie stets positiv.
Das Minimum  liegt bei
liegt bei 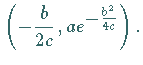
Wendepunkte und Asymptoten gibt es nicht.
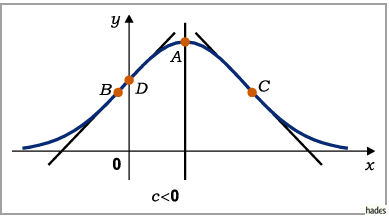
Fall
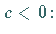 Die
Die  -Achse ist Asymptote. Das Maximum
-Achse ist Asymptote. Das Maximum  liegt bei
liegt bei
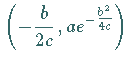 .
.
Die Wendepunkte 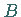 und
und 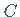 liegen bei
liegen bei
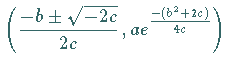 .
.
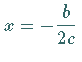 dar, wobei die
dar, wobei die 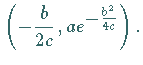
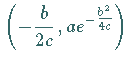 .
.
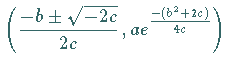 .
.