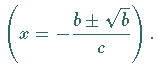Produkt aus Potenz- und Exponentialfunktion
Die Funktion
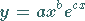 |
(2.62) |
wird hier nur für den Fall 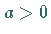 betrachtet, da sich ihre Kurve zu
betrachtet, da sich ihre Kurve zu 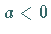 durch
Spiegelung an der
durch
Spiegelung an der  -Achse ergibt, und nur für den Fall positiver
-Achse ergibt, und nur für den Fall positiver  -Werte, so
daß sie stets positiv bleibt.
Die folgenden 8 Abbildungen zeigen, daß durch geeignete Kombination der Parameter die
unterschiedlichsten Kurvenverläufe dargestellt werden können.
-Werte, so
daß sie stets positiv bleibt.
Die folgenden 8 Abbildungen zeigen, daß durch geeignete Kombination der Parameter die
unterschiedlichsten Kurvenverläufe dargestellt werden können.
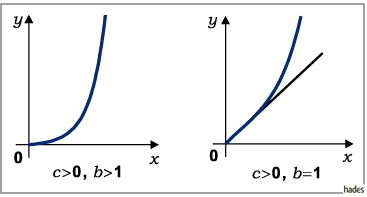
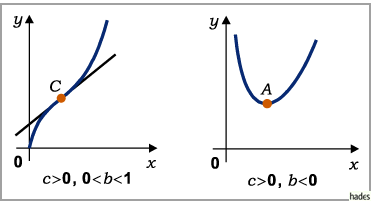
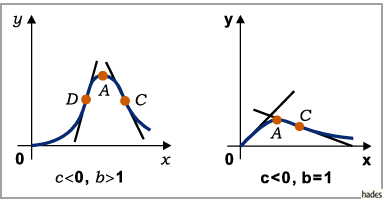
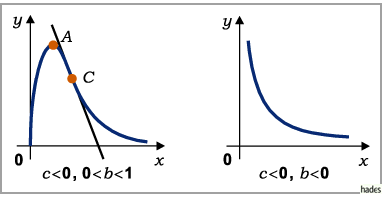
Für 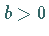 verläuft die Kurve durch den Koordinatenursprung.
Tangente ist in diesem Punkt für
verläuft die Kurve durch den Koordinatenursprung.
Tangente ist in diesem Punkt für 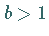 die
die  -Achse, für
-Achse, für  die
Winkelhalbierende
die
Winkelhalbierende 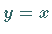 des ersten Quadranten und für
des ersten Quadranten und für 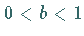 die
die 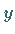 -Achse.
-Achse.
Für 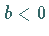 ist die
ist die 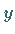 -Achse Asymptote.
Für
-Achse Asymptote.
Für 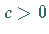 wächst die Funktion mit
wächst die Funktion mit  über alle Grenzen, für
über alle Grenzen, für 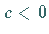 geht sie
asymptotisch gegen 0.
geht sie
asymptotisch gegen 0.
Für verschiedene Vorzeichen von 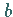 und
und 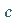 besitzt die Funktion ein Extremum
besitzt die Funktion ein Extremum  bei
bei
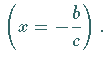 Die Kurve besitzt entweder keinen, einen oder zwei Wendepunkte
Die Kurve besitzt entweder keinen, einen oder zwei Wendepunkte 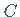 und
und 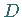 bei
bei
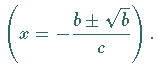
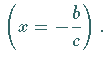 Die Kurve besitzt entweder keinen, einen oder zwei Wendepunkte
Die Kurve besitzt entweder keinen, einen oder zwei Wendepunkte