Exponentialsumme
Die Funktion
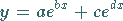 |
(2.60) |
ist in den folgenden vier Abbildungen für charakteristische Vorzeichen-Relationen
dargestellt.
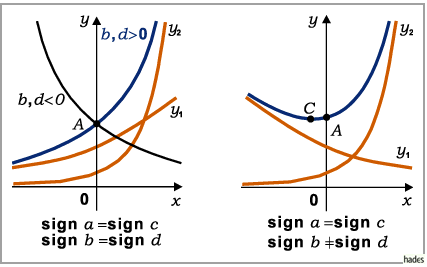
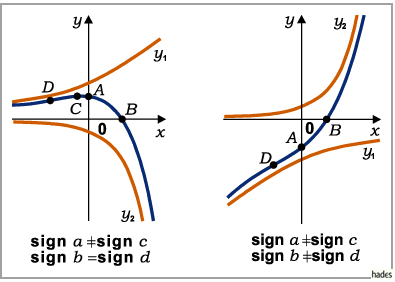
Die Konstruktion der Kurve erfolgt über die Addition der Ordinaten der Kurven der
beiden Summanden 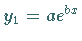 und
und 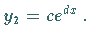
Die Funktion ist stetig. Wenn keine der Zahlen 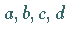 gleich 0 ist, besitzt die
Kurve eine der vier dargestellten Formen.
Die Kurvenbilder können in Abhängigkeit von den Vorzeichen der Parameter an den
Koordinatenachsen gespiegelt sein.
gleich 0 ist, besitzt die
Kurve eine der vier dargestellten Formen.
Die Kurvenbilder können in Abhängigkeit von den Vorzeichen der Parameter an den
Koordinatenachsen gespiegelt sein.
Die Schnittpunkte  und
und 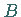 mit der
mit der 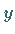 - bzw.
- bzw.  -Achse liegen bei
-Achse liegen bei 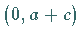 bzw.
bzw.
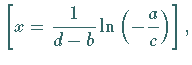 das Extremum
das Extremum 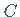 bei
bei
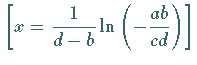 und der Wendepunkt
und der Wendepunkt 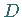 bei
bei
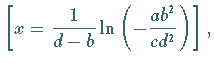 soweit diese
Punkte vorhanden sind.
soweit diese
Punkte vorhanden sind.
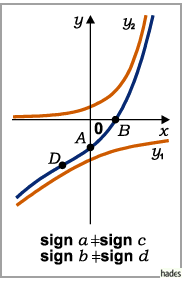
Fall a)
Die Parameter  und
und 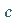 bzw.
bzw. 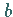 und
und 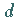 besitzen gleiches Vorzeichen:
Die Funktion erfährt keinen Vorzeichenwechsel; sie ändert sich von 0 bis
besitzen gleiches Vorzeichen:
Die Funktion erfährt keinen Vorzeichenwechsel; sie ändert sich von 0 bis 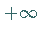 bzw.
bzw. 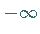 oder von
oder von 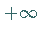 bzw.
bzw.  bis 0.
Wendepunkte gibt es keine; Asymptote ist die
bis 0.
Wendepunkte gibt es keine; Asymptote ist die  -Achse.
-Achse.
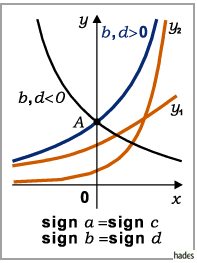
Fall b)
Die Parameter  und
und 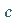 haben gleiche,
haben gleiche, 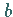 und
und 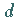 verschiedene Vorzeichen:
Die Funktion ändert sich ohne Vorzeichenwechsel von
verschiedene Vorzeichen:
Die Funktion ändert sich ohne Vorzeichenwechsel von 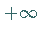 bis
bis 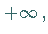 wobei
sie ein Minimum durchläuft, bzw. von
wobei
sie ein Minimum durchläuft, bzw. von 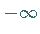 bis
bis  ,
dabei ein Maximum
durchlaufend. Wendepunkte gibt es keine.
,
dabei ein Maximum
durchlaufend. Wendepunkte gibt es keine.
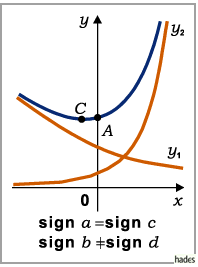
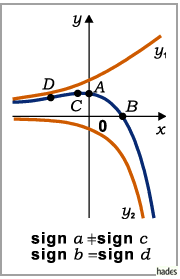
Fall c)
Die Parameter  und
und 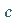 haben verschiedene,
haben verschiedene, 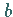 und
und 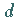 gleiche Vorzeichen:
Die Funktion ändert sich von 0 bis
gleiche Vorzeichen:
Die Funktion ändert sich von 0 bis 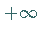 bzw.
bzw. 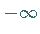 oder von
oder von 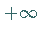 bzw.
bzw.
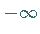 bis 0, wobei sie einmal ihr Vorzeichen wechselt und ein Extremum
bis 0, wobei sie einmal ihr Vorzeichen wechselt und ein Extremum 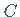 und einen
Wendepunkt
und einen
Wendepunkt 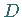 durchläuft.
Die
durchläuft.
Die  -Achse ist Asymptote.
-Achse ist Asymptote.
Fall d)
Die Parameter  und
und 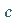 und auch
und auch 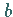 und
und 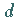 besitzen unterschiedliche Vorzeichen:
Die Funktion ändert sich monoton zwischen
besitzen unterschiedliche Vorzeichen:
Die Funktion ändert sich monoton zwischen 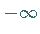 und
und 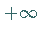 bzw. zwischen
bzw. zwischen
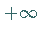 und
und 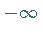 .
Sie besitzt keine Extrema, aber einen Wendepunkt
.
Sie besitzt keine Extrema, aber einen Wendepunkt 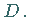
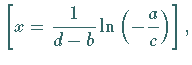 das Extremum
das Extremum 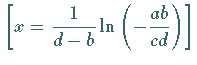 und der Wendepunkt
und der Wendepunkt 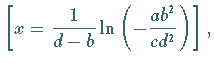 soweit diese
Punkte vorhanden sind.
soweit diese
Punkte vorhanden sind.