Kurve 3. Ordnung, Typ III
Die Funktion
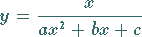 |
(2.49) |
beschreibt eine Kurve 3. Ordnung durch den Koordinatenursprung mit der  -Achse
als Asymptote.
-Achse
als Asymptote.
Der Verlauf der Funktion hängt von den Vorzeichen von  und von
und von 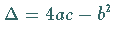 sowie von den Vorzeichen der Wurzeln
sowie von den Vorzeichen der Wurzeln 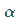 und
und 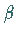 der Gleichung
der Gleichung 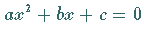 ab, wenn
ab, wenn 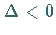 ist, vom Vorzeichen von
ist, vom Vorzeichen von 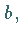 wenn
wenn 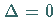 ist.
Von den zwei Fällen
ist.
Von den zwei Fällen 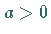 und
und 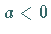 wird hier nur der erste betrachtet, da sich der
zweite durch Spiegelung der Kurve für
wird hier nur der erste betrachtet, da sich der
zweite durch Spiegelung der Kurve für 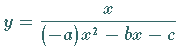 an der
an der  -Achse
ergibt.
-Achse
ergibt.
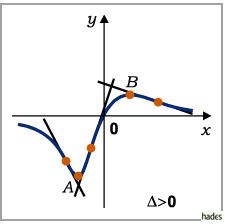
a) Fall
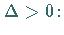 Die Funktion verläuft stetig, nimmt von
Die Funktion verläuft stetig, nimmt von 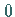 bis zum Minimum ab, steigt dann bis zum
Maximum an, um danach wieder auf
bis zum Minimum ab, steigt dann bis zum
Maximum an, um danach wieder auf 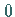 abzufallen.
abzufallen.
Die Extremwerte  und
und 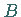 liegen bei
liegen bei
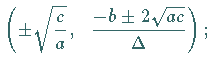 es gibt drei Wendepunkte.
es gibt drei Wendepunkte.
b) Fall
 Der Verlauf hängt vom Vorzeichen von
Der Verlauf hängt vom Vorzeichen von 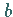 ab:
ab:
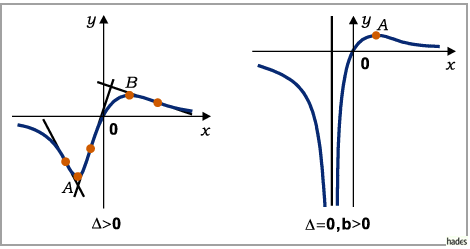
c) Fall
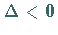
 Die Funktion besitzt zwei Unstetigkeitsstellen und zwar bei
Die Funktion besitzt zwei Unstetigkeitsstellen und zwar bei  und
und
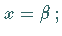 ihr Verlauf hängt von den Vorzeichen von
ihr Verlauf hängt von den Vorzeichen von 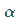 und
und 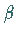 ab.
ab.
- Die Vorzeichen von
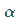 und
und 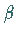 sind verschieden:
Die Funktion nimmt von
sind verschieden:
Die Funktion nimmt von 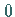 bis
bis 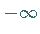 ab, springt auf
ab, springt auf 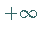 ,
nimmt
wieder von
,
nimmt
wieder von 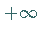 bis
bis 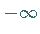 ab, wobei sie durch den Koordinatenursprung
verläuft, erfährt einen zweiten Sprung nach
ab, wobei sie durch den Koordinatenursprung
verläuft, erfährt einen zweiten Sprung nach 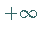 ,
von wo sie gegen
,
von wo sie gegen
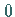 abfällt.
Extremwerte treten nicht auf.
abfällt.
Extremwerte treten nicht auf.
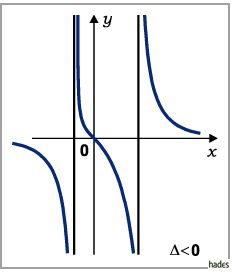
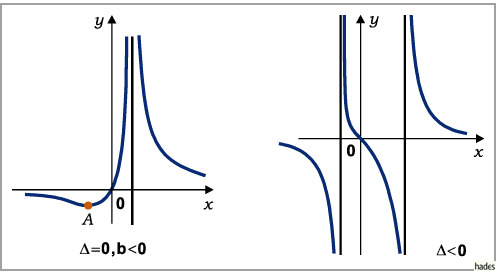
- Die Vorzeichen von
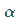 und
und 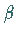 sind beide negativ:
Die Funktion nimmt von
sind beide negativ:
Die Funktion nimmt von 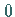 bis
bis 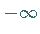 ab, springt auf
ab, springt auf 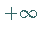 ,
läuft
von hier über ein Minimum wieder bis auf
,
läuft
von hier über ein Minimum wieder bis auf 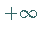 ,
springt abermals auf
,
springt abermals auf
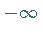 ,
steigt dann bis zum Maximum an, um danach asymptotisch gegen
,
steigt dann bis zum Maximum an, um danach asymptotisch gegen 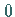 abzufallen.
abzufallen.
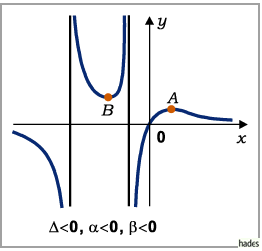
Die Extremwerte  und
und 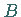 werden nach den gleichen Formeln wie im
Fall
werden nach den gleichen Formeln wie im
Fall 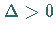 berechnet.
berechnet.
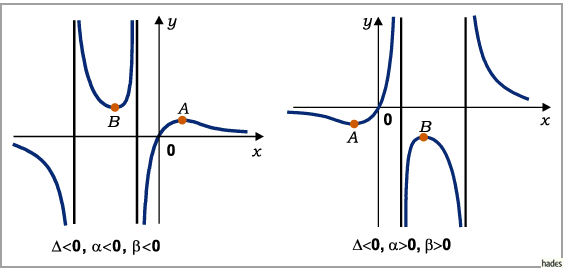
- Die Vorzeichen von
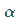 und
und 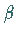 sind beide positiv:
Die Funktion nimmt von
sind beide positiv:
Die Funktion nimmt von 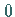 bis zum Minimum ab, wächst dann auf
bis zum Minimum ab, wächst dann auf 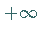 an,
springt auf
an,
springt auf 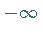 ,
durchläuft ein Maximum, um wieder
,
durchläuft ein Maximum, um wieder 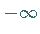 zu
erreichen, springt auf
zu
erreichen, springt auf 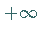 und verläuft von hier gegen
und verläuft von hier gegen 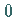 .
.
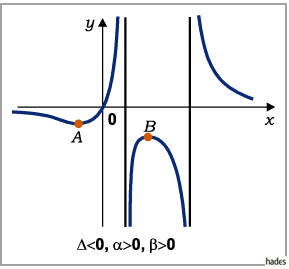
Die Extremwerte  und
und 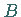 werden nach den gleichen Formeln wie im
Fall
werden nach den gleichen Formeln wie im
Fall  berechnet.
berechnet.
In allen drei Fällen besitzt die Kurve einen Wendepunkt.
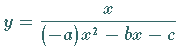 an der
an der 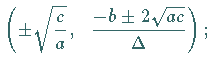 es gibt drei Wendepunkte.
es gibt drei Wendepunkte.
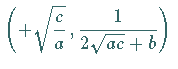 .
.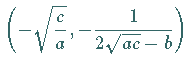 .
.
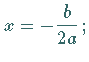 beide
Kurven besitzen je einen Wendepunkt.
beide
Kurven besitzen je einen Wendepunkt.