Kurve 3. Ordnung, Typ II
Die Funktion
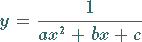 |
(2.48) |
beschreibt eine Kurve 3. Ordnung , die symmetrisch zu der vertikalen Geraden bei
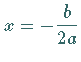 verläuft und die die
verläuft und die die  -Achse zur Asymptote hat.
-Achse zur Asymptote hat.
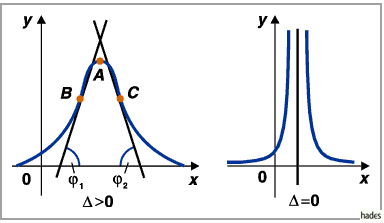
Ihr Verhalten hängt von den Vorzeichen von  und
und 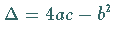 ab.
Von den zwei Fällen
ab.
Von den zwei Fällen 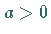 und
und 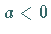 wird hier nur der erste betrachtet,
da der zweite durch Spiegelung von
wird hier nur der erste betrachtet,
da der zweite durch Spiegelung von 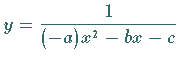 an der
an der
 -Achse erhalten werden kann.
-Achse erhalten werden kann.
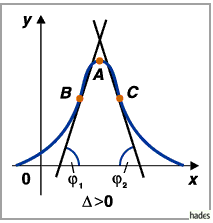
a) Fall
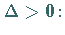 Die Funktion ist für beliebiges
Die Funktion ist für beliebiges  positiv und stetig und wächst von
positiv und stetig und wächst von 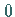 bis zum Maximum, um dann wieder gegen
bis zum Maximum, um dann wieder gegen 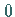 zu fallen.
Das Maximum
zu fallen.
Das Maximum  liegt bei
liegt bei 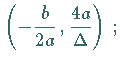 die
Wendepunkte
die
Wendepunkte 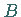 und
und 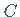 liegen bei
liegen bei
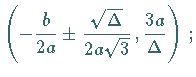 die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu
die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu
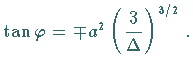
b) Fall
 Die Funktion ist für beliebiges
Die Funktion ist für beliebiges  positiv, wächst von
positiv, wächst von 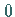 bis
bis 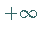 ,
besitzt bei
,
besitzt bei 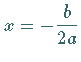 eine Unstetigkeitsstelle mit
eine Unstetigkeitsstelle mit 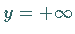 und
nimmt von hier wieder auf
und
nimmt von hier wieder auf 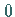 ab.
ab.
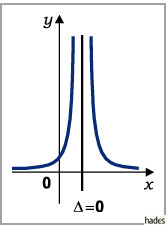
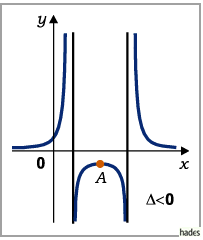
c) Fall
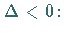 Die Funktion wächst von
Die Funktion wächst von 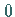 bis
bis 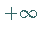 ,
springt an der Unstetigkeitsstelle
auf
,
springt an der Unstetigkeitsstelle
auf 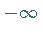 ,
um von hier über ein Maximum wieder nach
,
um von hier über ein Maximum wieder nach 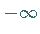 zu verlaufen,
von wo es einen zweiten Sprung nach
zu verlaufen,
von wo es einen zweiten Sprung nach 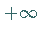 gibt, auf den schließlich ein
Abfall gegen
gibt, auf den schließlich ein
Abfall gegen 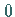 folgt.
Das Maximum
folgt.
Das Maximum  liegt bei
liegt bei 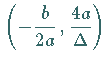 ;
die Unstetigkeitsstellen liegen bei
;
die Unstetigkeitsstellen liegen bei 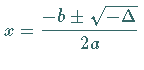 .
.

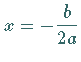 verläuft und die die
verläuft und die die 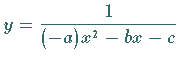 an der
an der
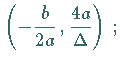 die
Wendepunkte
die
Wendepunkte 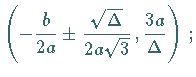 die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu
die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu
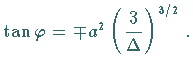
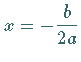 eine Unstetigkeitsstelle mit
eine Unstetigkeitsstelle mit 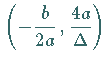 ;
die Unstetigkeitsstellen liegen bei
;
die Unstetigkeitsstellen liegen bei 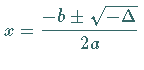 .
.