|
Es sind die Unstetigkeitsstellen der Funktion
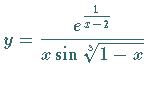 zu ermitteln.
Der Exponent
zu ermitteln.
Der Exponent 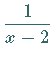 besitzt an der Stelle
besitzt an der Stelle 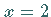 einen unendlichen
Sprung; für
einen unendlichen
Sprung; für 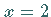 hat auch
hat auch 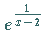 einen unendlichen Sprung:
einen unendlichen Sprung:
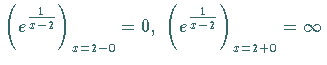 .
Die Funktion .
Die Funktion 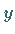 hat bei
hat bei 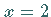 einen endlichen Nenner. Folglich gibt es für
einen endlichen Nenner. Folglich gibt es für
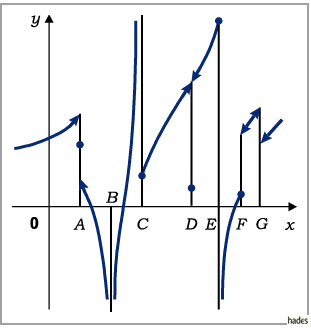
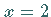 einen unendlichen Sprung vom gleichen Typ, wie im Punkt
einen unendlichen Sprung vom gleichen Typ, wie im Punkt 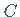 der folgenden
Abbildung:
der folgenden
Abbildung:
Für 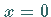 wird der Nenner zu null, ebenso für die
wird der Nenner zu null, ebenso für die  -Werte, für die -Werte, für die
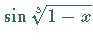 zu null wird.
Letztere entsprechen den Wurzeln der Gleichung
zu null wird.
Letztere entsprechen den Wurzeln der Gleichung 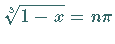 oder
oder
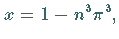 wobei
wobei 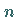 eine beliebige ganze Zahl ist.
Der Zähler wird für keinen dieser Werte zu null, so daß die Funktion an den
Stellen
eine beliebige ganze Zahl ist.
Der Zähler wird für keinen dieser Werte zu null, so daß die Funktion an den
Stellen 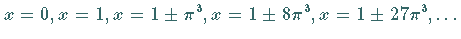 Unstetigkeitsstellen der gleichen Art hat wie der Punkt
Unstetigkeitsstellen der gleichen Art hat wie der Punkt 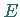 in der obigen Abbildung.
in der obigen Abbildung.
| 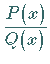 mit den Polynomen
mit den Polynomen
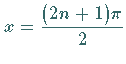 unendliche Sprünge;
unendliche Sprünge;