Definition der Stetigkeit
Eine Funktion 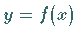 heißt an der Stelle
heißt an der Stelle  stetig , wenn
stetig , wenn
1. 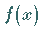 an der Stelle
an der Stelle  definiert ist und
definiert ist und
2. der Grenzwert 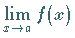 existiert und gleich
existiert und gleich 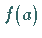 ist.
ist.
Das ist genau dann der Fall, wenn es zu jedem vorgegebenen 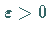 ein
ein
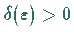 gibt, so daß
gibt, so daß
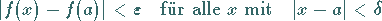 |
(2.30) |
gilt.
Man spricht von einseitiger ( links - oder rechtsseitiger )
Stetigkeit , wenn anstelle von 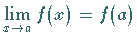 nur einer der beiden
Grenzwerte
nur einer der beiden
Grenzwerte
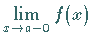 oder
oder 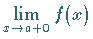 existiert und
gleich
existiert und
gleich 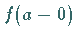 oder
oder 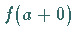 ist.
ist.
Wenn eine Funktion für alle Werte  in einem gegebenen Intervall von
in einem gegebenen Intervall von  bis
bis 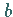 stetig ist, dann wird die Funktion stetig in diesem Intervall genannt, das als
Zahlenintervall offen, halboffen oder abgeschlossen sein kann.
Ist eine Funktion für alle Punkte der Zahlengerade definiert und stetig, dann heißt
sie überall stetig .
stetig ist, dann wird die Funktion stetig in diesem Intervall genannt, das als
Zahlenintervall offen, halboffen oder abgeschlossen sein kann.
Ist eine Funktion für alle Punkte der Zahlengerade definiert und stetig, dann heißt
sie überall stetig .
Eine Funktion besitzt für den Wert 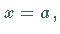 der sich im Inneren oder auf dem Rande des
Definitionsbereiches befindet, eine Unstetigkeitsstelle , wenn dort die Funktion
nicht definiert ist oder wenn
der sich im Inneren oder auf dem Rande des
Definitionsbereiches befindet, eine Unstetigkeitsstelle , wenn dort die Funktion
nicht definiert ist oder wenn 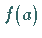 nicht mit dem Grenzwert
nicht mit dem Grenzwert 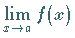 übereinstimmt bzw. dieser Grenzwert nicht existiert.
Wenn die Funktion nur auf einer Seite von
übereinstimmt bzw. dieser Grenzwert nicht existiert.
Wenn die Funktion nur auf einer Seite von  definiert ist, z.B.
definiert ist, z.B. 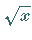 für
für
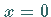 und
und 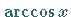 für
für 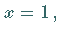 dann wird nicht von einer Unstetigkeitsstelle,
sondern von einem Abbrechen der Funktion gesprochen.
dann wird nicht von einer Unstetigkeitsstelle,
sondern von einem Abbrechen der Funktion gesprochen.
Eine Funktion 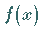 wird stückweise stetig genannt, wenn sie in allen Punkten
eines Intervalls mit Ausnahme endlich vieler einzelner Punkte stetig ist und in ihren
Unstetigkeitsstellen endliche Sprünge besitzt.
wird stückweise stetig genannt, wenn sie in allen Punkten
eines Intervalls mit Ausnahme endlich vieler einzelner Punkte stetig ist und in ihren
Unstetigkeitsstellen endliche Sprünge besitzt.