Kardioide
Die Kardioide kann auf zweierlei Weise definiert werden:
1. als Spezialfall der PASCALschen Schnecke mit
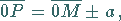 |
(2.225) |
wobei  der Durchmesser des Kreises ist, oder
der Durchmesser des Kreises ist, oder
2. als Epizykloide mit gleich großem
Durchmesser  des festen und des beweglichen Kreises.
des festen und des beweglichen Kreises.
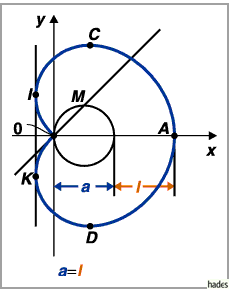
Die Gleichung lautet in kartesischen Koordinaten, in Parameterform sowie in
Polarkoordinaten:
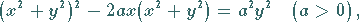 |
(2.226a) |
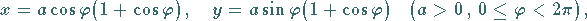 |
(2.226b) |
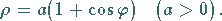 |
(2.226c) |
Der Koordinatenursprung ist ein Rückkehrpunkt.
Der Scheitel  liegt bei
liegt bei 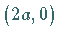 ;
Maximum
;
Maximum 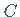 und Minimum
und Minimum 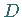 liegen bei
liegen bei
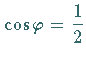 mit den Koordinaten
mit den Koordinaten
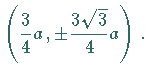
Der Flächeninhalt beträgt 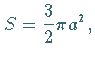 d.h. die sechsfache
Fläche des Kreises mit dem Durchmesser
d.h. die sechsfache
Fläche des Kreises mit dem Durchmesser  Die Kurvenlänge ist
Die Kurvenlänge ist 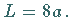
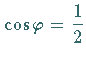 mit den Koordinaten
mit den Koordinaten
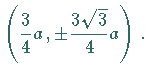
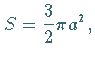 d.h. die sechsfache
Fläche des Kreises mit dem Durchmesser
d.h. die sechsfache
Fläche des Kreises mit dem Durchmesser