Pascalsche Schnecke
Einen weiteren Spezialfall der allgemeinen Konchoide, die
Konchoide des Kreises , mit der Bedingung 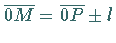 (2.221), wobei der Koordinatenursprung auf dem Kreis liegt, nennt man
PASCALsche Schnecke .
(2.221), wobei der Koordinatenursprung auf dem Kreis liegt, nennt man
PASCALsche Schnecke .
Die Gleichung lautet in kartesischen und Polarkoordinaten sowie in Parameterform:
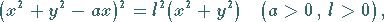 |
(2.224a) |
 |
(2.224b) |
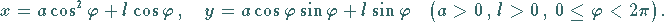 |
(2.224c) |
Dabei ist  der Durchmesser des Kreises.
der Durchmesser des Kreises.
Die Scheitel  und
und 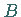 liegen bei
liegen bei 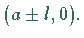 Die Form der Kurve hängt von den Größen
Die Form der Kurve hängt von den Größen  und
und 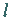 ab, wie man aus den drei
Abbildungen für die Konchoide des Kreises erkennen kann.
ab, wie man aus den drei
Abbildungen für die Konchoide des Kreises erkennen kann.
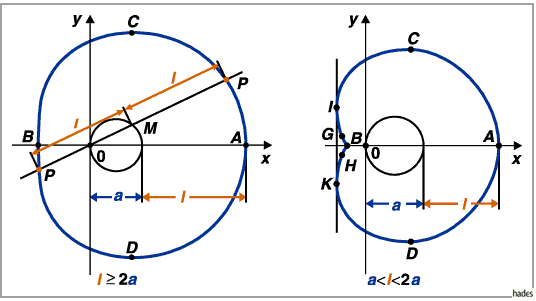
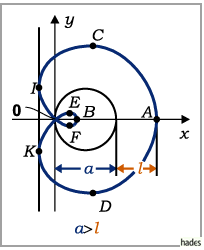
1. Extremwerte und Wendepunkte:
Für 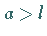 hat die Kurve vier Extremwerte
hat die Kurve vier Extremwerte 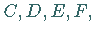 für
für 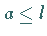 zwei; sie
liegen bei
zwei; sie
liegen bei 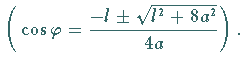
Für 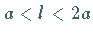 existieren zwei Wendepunkte
existieren zwei Wendepunkte 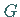 und
und 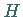 bei
bei
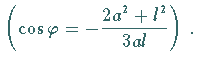
2. Doppeltangenten:
Für 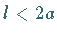 gibt es in den Punkten
gibt es in den Punkten 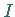 und
und 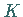 und zwar bei
und zwar bei
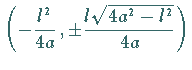 eine gemeinsame Tangente.
eine gemeinsame Tangente.
3. Singulärer Punkt: Der Koordinatenursprung ist ein singulärer
Punkt.
Für 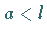 ist er ein isolierter Punkt, für
ist er ein isolierter Punkt, für 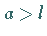 ein Doppelpunkt mit den
Tangentenrichtungen
ein Doppelpunkt mit den
Tangentenrichtungen 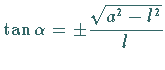 und dem
Krümmungsradius
und dem
Krümmungsradius 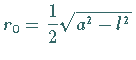 .
Für
.
Für  handelt es sich um einen Rückkehrpunkt; die Kurve nennt man
dann
Kardioide.
handelt es sich um einen Rückkehrpunkt; die Kurve nennt man
dann
Kardioide.
Der Flächeninhalt der Schnecke beträgt 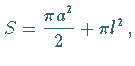 wobei im Falle
wobei im Falle 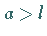 der Flächeninhalt der inneren Schleife nach dieser Formel
doppelt gezählt wird.
der Flächeninhalt der inneren Schleife nach dieser Formel
doppelt gezählt wird.
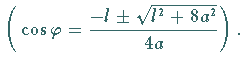
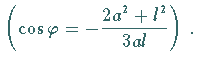
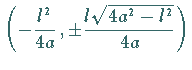 eine gemeinsame Tangente.
eine gemeinsame Tangente.
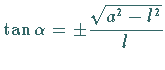 und dem
Krümmungsradius
und dem
Krümmungsradius 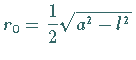 .
Für
.
Für 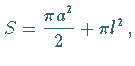 wobei im Falle
wobei im Falle