Kartesisches Blatt
Die Gleichung
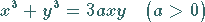 |
(2.216a) |
oder in Parameterform
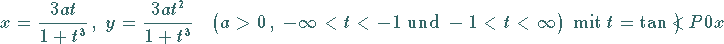 |
(2.216b) |
ergibt graphisch dargestellt das kartesische Blatt .
Dabei wird mit 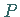 der Kurvenpunkt bezeichnet, der zum Parameterwert
der Kurvenpunkt bezeichnet, der zum Parameterwert 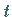 gehört,
und mit
gehört,
und mit 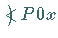 der Winkel, den die positive
der Winkel, den die positive  -Achse mit
-Achse mit 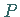 bildet.
bildet.
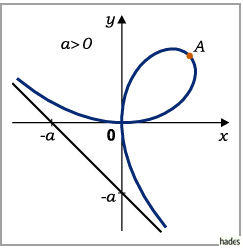
Der Koordinatenursprung ist infolge zweier ihn durchlaufender Kurvenzweige ein
Doppelpunkt, in dem beide Koordinatenachsen Tangenten sind.
Der Krümmungsradius ist für beide Kurvenzweige im Koordinatenursprung
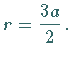 Die Asymptote berechnet sich aus
Die Asymptote berechnet sich aus 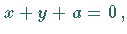 der Scheitelpunkt
der Scheitelpunkt  hat die
Koordinaten
hat die
Koordinaten 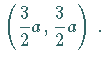
Der Flächeninhalt der Schleife ist 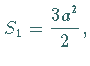 der Flächeninhalt
der Flächeninhalt
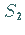 zwischen der Kurve und der Asymptote hat den gleichen Wert.
zwischen der Kurve und der Asymptote hat den gleichen Wert.
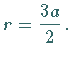 Die Asymptote berechnet sich aus
Die Asymptote berechnet sich aus 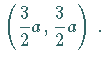
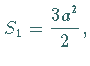 der Flächeninhalt
der Flächeninhalt