Vektordiagramm für Schwingungen
Die allgemeine Sinusfunktion (2.127, 2.128)
kann bequem mit den Polarkoordinaten 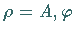 und den
kartesischen Koordinaten
und den
kartesischen Koordinaten 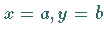 in einer Ebene dargestellt
werden.
Die Summe zweier solcher Größen ergibt sich dann als Summe der zwei
Summandenvektoren (linke Abbildung).
in einer Ebene dargestellt
werden.
Die Summe zweier solcher Größen ergibt sich dann als Summe der zwei
Summandenvektoren (linke Abbildung).
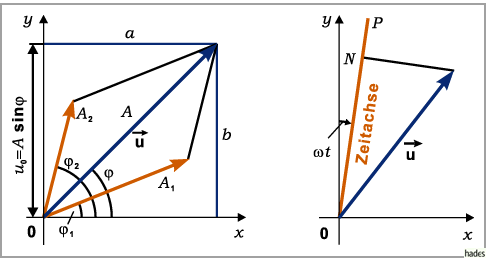
Entsprechend liefert die Summe mehrerer solcher Vektoren die Linearkombination
mehrerer allgemeiner Sinusfunktionen.
Diese Darstellung wird Vektordiagramm genannt.
Die Größe 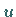 kann im Vektordiagramm für einen gegebenen Zeitpunkt
kann im Vektordiagramm für einen gegebenen Zeitpunkt 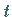 an Hand
der rechten Abbildung bestimmt werden:
an Hand
der rechten Abbildung bestimmt werden:
Zuerst wird durch den Koordinatenursprung O die Zeitachse 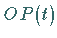 gelegt,
die mit konstanter Winkelgeschwindigkeit
gelegt,
die mit konstanter Winkelgeschwindigkeit 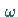 um O im Uhrzeigersinn
rotiert.
Zum Anfangszeitpunkt
um O im Uhrzeigersinn
rotiert.
Zum Anfangszeitpunkt  fallen
fallen 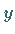 - und
- und 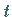 -Achse zusammen.
Danach ist in jedem Zeitpunkt
-Achse zusammen.
Danach ist in jedem Zeitpunkt 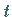 die Projektion
die Projektion 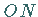 des Vektors
des Vektors  auf die
Zeitachse gleich dem Betrag der allgemeinen Sinusfunktion
auf die
Zeitachse gleich dem Betrag der allgemeinen Sinusfunktion
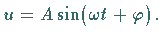 Zur Zeit
Zur Zeit  ist
ist 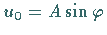 die Projektion auf die
die Projektion auf die 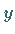 -Achse.
-Achse.