Dämpfung von Schwingungen
Die Funktion
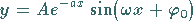 |
(2.131) |
liefert für 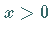 die Kurve einer gedämpften Schwingung .
die Kurve einer gedämpften Schwingung .
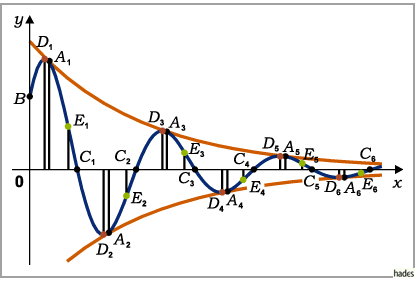
Die Schwingung erfolgt um die  -Achse, wobei sich die Kurve asymptotisch der
-Achse, wobei sich die Kurve asymptotisch der
 -Achse nähert.
Dabei wird die Sinuskurve von den beiden Exponentialkurven
-Achse nähert.
Dabei wird die Sinuskurve von den beiden Exponentialkurven 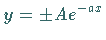 eingehüllt, indem sie diese in den Punkten
eingehüllt, indem sie diese in den Punkten
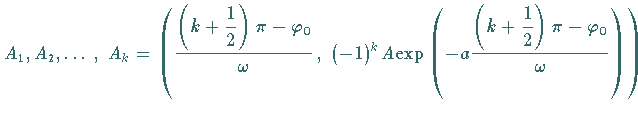
berühren.
Die Schnittpunkte mit den Koordinatenachsen sind
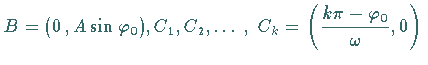 .
.
Die Extrema 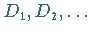 befinden sich bei
befinden sich bei
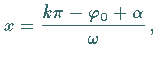 die Wendepunkte
die Wendepunkte 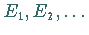 bei
bei 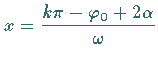 mit
mit
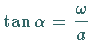 .
.
Als logarithmisches Dekrement der Dämpfung wird
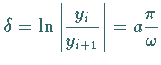 bezeichnet;
bezeichnet;
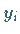 und
und 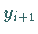 sind die Ordinaten zweier benachbarter Extrema.
sind die Ordinaten zweier benachbarter Extrema.
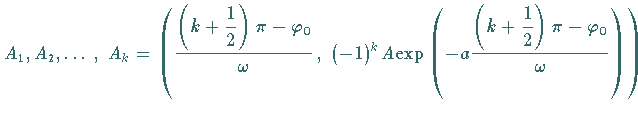
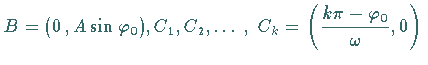 .
.
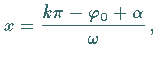 die Wendepunkte
die Wendepunkte 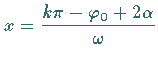 mit
mit
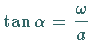 .
.
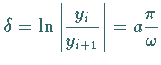 bezeichnet;
bezeichnet;