In der Technik und der Physik kommen oft zeitabhängige Größen der Form
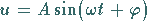 |
(2.127) |
vor.
Sie werden manchmal auch sinusoidale Größen genannt.
Ihre zeitabhängige Änderung beschreibt eine harmonische Schwingung .
Die graphische Darstellung dieser Gleichung liefert eine allgemeine Sinuskurve ,
wie sie die folgende Abbildung zeigt.
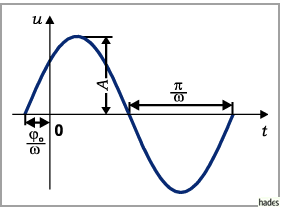
Die allgemeine Sinuskurve unterscheidet sich von der gewöhnlichen 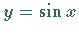 :
:
a) durch die Amplitude 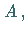 d.h. die größte Auslenkung von der
Zeitachse
d.h. die größte Auslenkung von der
Zeitachse 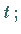
b) durch die Periode 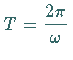 ,
die der
Wellenlänge entspricht (mit
,
die der
Wellenlänge entspricht (mit 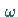 als Schwingungsfrequenz , die in der
Schwingungslehre Kreisfrequenz genannt wird);
als Schwingungsfrequenz , die in der
Schwingungslehre Kreisfrequenz genannt wird);
c) durch die Anfangsphase oder Phasenverschiebung mit dem
Anfangswinkel 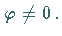
Die Größe 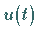 kann auch in der Form
kann auch in der Form
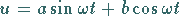 |
(2.128) |
dargestellt werden, mit 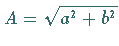 und
und 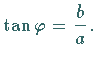 Die Größen
Die Größen 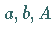 und
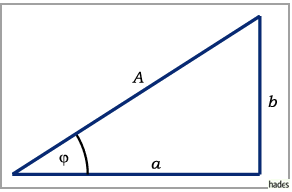
und 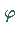 lassen sich in Übereinstimmung mit der
folgenden Abbildung als Bestimmungsstücke eines rechtwinkligen Dreiecks darstellen.
lassen sich in Übereinstimmung mit der
folgenden Abbildung als Bestimmungsstücke eines rechtwinkligen Dreiecks darstellen.
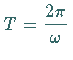 ,
die der
Wellenlänge entspricht (mit
,
die der
Wellenlänge entspricht (mit 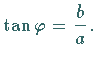 Die Größen
Die Größen