Ansatzverfahren

Als Näherungslösung für die Randwertaufgabe (19.118) wird eine Linearkombination geeignet gewählter Funktionen verwendet, die einzeln die Randbedingungen erfüllen und linear unabhängig sind:

(19.121)

(19.122)

auftreten. Die Bestimmung der Ansatzkoeffizienten kann nach folgenden Prinzipien erfolgen:
1. Kollokationsmethode: Der Defekt soll an Stellen , den Kollokationsstellen , verschwinden. Die Bedingungen

(19.123)

liefern ein lineares Gleichungssystem für die Ansatzkoeffizienten.
2. Fehlerquadratmethode:Man fordert, daß das Integral

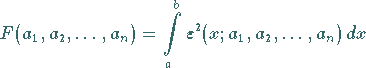(19.124)

in Abhängigkeit von den Koeffizienten minimal wird. Die notwendigen Bedingungen

(19.125)

ergeben ein lineares Gleichungssystem für die Koeffizienten .
3. Galerkin-Verfahren: Man fordert die sogenannte Fehlerorthogonalität , d.h., es muß

(19.126)

gelten, und erhält auch auf diese Weise ein lineares Gleichungssystem zur Bestimmung der Ansatzkoeffizienten.
4. Ritz-Verfahren:Bei vielen Randwertaufgaben hat die Lösung die Eigenschaft, auch Lösung einer sogenannten Variationsaufgabe zu sein, d.h., macht ein Integral der Form

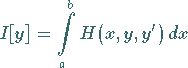(19.127)

zum Minimum (s. (10.4)). Kennt man die Funktion , so ersetzt man gemäß (19.121) näherungsweise durch und macht zum Minimum. Die dafür notwendigen Bedingungen

(19.128)

liefern Gleichungen für die Koeffizienten .

Beispiel
	Unter bestimmten Voraussetzungen an die Funktionen und sind die Randwertaufgabe

(19.129)

(19.130)

(19.131)

(19.132)

(19.133)