Mit dem Schießverfahren wird die Lösung von Randwertaufgaben auf die Lösung
von Anfangswertaufgaben zurückgeführt.
Das Prinzip soll am sogenannten einfachen Schießverfahren , auch
Einzielverfahren genannt, beschrieben werden.
1. Einzielverfahren:
Der Randwertaufgabe (19.118) wird die Anfangswertaufgabe
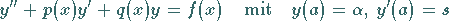 |
(19.134) |
zugeordnet.
Dabei ist 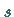 ein Parameter, von dem die Lösung
ein Parameter, von dem die Lösung 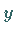 der Anfangswertaufgabe
(19.134) abhängt, d.h., es gilt
der Anfangswertaufgabe
(19.134) abhängt, d.h., es gilt 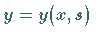 .
Die Funktion
.
Die Funktion 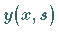 erfüllt gemäß (19.134) die erste
Randbedingung
erfüllt gemäß (19.134) die erste
Randbedingung 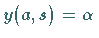 .
Der Parameter
.
Der Parameter 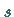 ist so zu bestimmen, daß
ist so zu bestimmen, daß 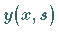 auch die zweite Randbedingung
auch die zweite Randbedingung
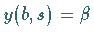 erfüllt.
Dazu ist die Gleichung
erfüllt.
Dazu ist die Gleichung
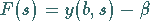 |
(19.135) |
zweckmäßigerweise mit Hilfe der Regula falsi zu lösen.
Diese benötigt nur Funktionswerte 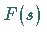 ,
aber jede Funktionswertberechnung erfordert
die Lösung der Anfangswertaufgabe (19.134) nach einem der im
Abschnitt Anfangswertaufgaben
angegebenen Verfahren bis
,
aber jede Funktionswertberechnung erfordert
die Lösung der Anfangswertaufgabe (19.134) nach einem der im
Abschnitt Anfangswertaufgaben
angegebenen Verfahren bis 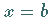 für den speziellen Parameterwert
für den speziellen Parameterwert 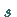 .
.
2. Mehrzielverfahren:
Bei der sogenannten Mehrzielmethode wird das Integrationsintervall 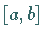 in
Teilintervalle zerlegt und auf jedem Teilintervall die Einzielmethode angewendet.
Damit setzt sich die gesuchte Lösung aus Teillösungen zusammen, deren stetiger
Übergang an den Teilintervallgrenzen zu sichern ist.
Diese Forderung ergibt zusätzliche Bedingungen.
Zur numerischen Realisierung der Mehrzielmethode, die vor allem bei nichtlinearen
Randwertaufgaben verwendet wird, s. Lit. 19.12.
in
Teilintervalle zerlegt und auf jedem Teilintervall die Einzielmethode angewendet.
Damit setzt sich die gesuchte Lösung aus Teillösungen zusammen, deren stetiger
Übergang an den Teilintervallgrenzen zu sichern ist.
Diese Forderung ergibt zusätzliche Bedingungen.
Zur numerischen Realisierung der Mehrzielmethode, die vor allem bei nichtlinearen
Randwertaufgaben verwendet wird, s. Lit. 19.12.
![]() ,
aber jede Funktionswertberechnung erfordert
die Lösung der Anfangswertaufgabe (19.134) nach einem der im
Abschnitt Anfangswertaufgaben
angegebenen Verfahren bis
,
aber jede Funktionswertberechnung erfordert
die Lösung der Anfangswertaufgabe (19.134) nach einem der im
Abschnitt Anfangswertaufgaben
angegebenen Verfahren bis ![]() für den speziellen Parameterwert
für den speziellen Parameterwert ![]() .
.
![]() in
Teilintervalle zerlegt und auf jedem Teilintervall die Einzielmethode angewendet.
Damit setzt sich die gesuchte Lösung aus Teillösungen zusammen, deren stetiger
Übergang an den Teilintervallgrenzen zu sichern ist.
Diese Forderung ergibt zusätzliche Bedingungen.
Zur numerischen Realisierung der Mehrzielmethode, die vor allem bei nichtlinearen
Randwertaufgaben verwendet wird, s. Lit. 19.12.
in
Teilintervalle zerlegt und auf jedem Teilintervall die Einzielmethode angewendet.
Damit setzt sich die gesuchte Lösung aus Teillösungen zusammen, deren stetiger
Übergang an den Teilintervallgrenzen zu sichern ist.
Diese Forderung ergibt zusätzliche Bedingungen.
Zur numerischen Realisierung der Mehrzielmethode, die vor allem bei nichtlinearen
Randwertaufgaben verwendet wird, s. Lit. 19.12.