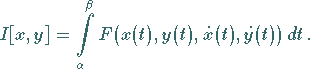Aufgabenstellung
1. Extremum eines Integralausdrucks
In der Differentialrechnung besteht eine wichtige Aufgabe darin, festzustellen, für
welche 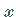 -Werte eine vorgegebene Funktion
-Werte eine vorgegebene Funktion 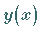 einen Extremwert hat.
In der Variationsrechnung lautet die entsprechende Frage:
Für welche Funktionen nimmt ein bestimmtes Integral, dessen Integrand von dieser
Funktion und deren Ableitungen abhängt, einen Extremwert an?
In der Variationsrechnung wird demzufolge ein ganzer Funktionsverlauf
einen Extremwert hat.
In der Variationsrechnung lautet die entsprechende Frage:
Für welche Funktionen nimmt ein bestimmtes Integral, dessen Integrand von dieser
Funktion und deren Ableitungen abhängt, einen Extremwert an?
In der Variationsrechnung wird demzufolge ein ganzer Funktionsverlauf 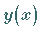 gesucht, der
einen Integralausdruck der Form
gesucht, der
einen Integralausdruck der Form
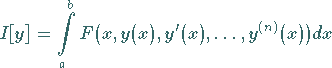 |
(10.1) |
zum Extremum macht, wenn 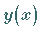 eine bestimmte, genau charakterisierte Funktionenklasse
durchläuft.
Dabei können für die Funktionen
eine bestimmte, genau charakterisierte Funktionenklasse
durchläuft.
Dabei können für die Funktionen 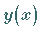 und deren Ableitungen noch zusätzliche
Bedingungen, sogenannte Rand - und Nebenbedingungen , gestellt werden.
und deren Ableitungen noch zusätzliche
Bedingungen, sogenannte Rand - und Nebenbedingungen , gestellt werden.
2. Integralausdrücke der Variationsrechnung
An Stelle der unabhängigen Variablen 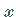 können in (10.1) auch mehrere
Variablen stehen.
Die auftretenden Ableitungen sind dann partielle Ableitungen, und das Integral in
(10.1) entspricht einem mehrfachen Integral.
Im wesentlichen werden in der Variationsrechnung Aufgaben mit folgenden
Integralausdrücken untersucht:
können in (10.1) auch mehrere
Variablen stehen.
Die auftretenden Ableitungen sind dann partielle Ableitungen, und das Integral in
(10.1) entspricht einem mehrfachen Integral.
Im wesentlichen werden in der Variationsrechnung Aufgaben mit folgenden
Integralausdrücken untersucht:
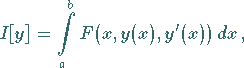 |
(10.2) |
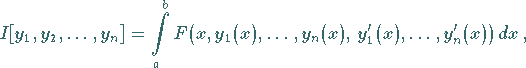 |
(10.3) |
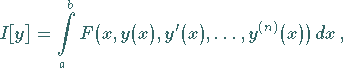 |
(10.4) |
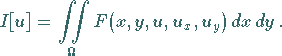 |
(10.5) |
Die gesuchte Funktion ist 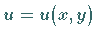 ,
und
,
und  stellt einen ebenen
Integrationsbereich dar.
stellt einen ebenen
Integrationsbereich dar.
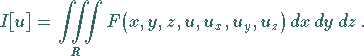 |
(10.6) |
Die gesuchte Funktion ist 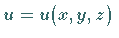 ,
und
,
und 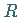 stellt einen räumlichen
Integrationsbereich dar.
stellt einen räumlichen
Integrationsbereich dar.
Für die Lösungen eines Variationsproblems können zusätzliche Randbedingungen
vorgegeben sein, die im eindimensionalen Fall an den Intervallrändern 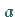 und
und 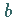 bzw.
auf dem Rand des Integrationsgebietes
bzw.
auf dem Rand des Integrationsgebietes 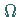 im zweidimensionalen Fall gelten sollen.
Darüber hinaus können den Lösungen noch verschiedene Arten von
Nebenbedingungen , z.B. in Integralform oder als Differentialgleichung vorgeschrieben
sein.
im zweidimensionalen Fall gelten sollen.
Darüber hinaus können den Lösungen noch verschiedene Arten von
Nebenbedingungen , z.B. in Integralform oder als Differentialgleichung vorgeschrieben
sein.
Ein Variationsproblem heißt von erster bzw. höherer Ordnung je nachdem,
ob die Funktion 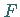 im Integralausdruck der Variationsaufgabe nur die erste Ableitung
im Integralausdruck der Variationsaufgabe nur die erste Ableitung 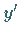 oder höhere Ableitungen
oder höhere Ableitungen 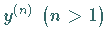 der Funktion
der Funktion 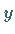 enthält.
enthält.
3. Parameterdarstellung der Variationsaufgabe
Ein Variationsproblem kann auch in Parameterdarstellung vorliegen.
Für die Kurvendarstellung
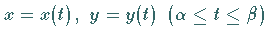 hat dann z.B. der
Integralausdruck (10.2) die Form
hat dann z.B. der
Integralausdruck (10.2) die Form
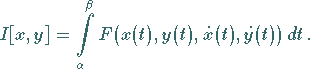 |
(10.7) |
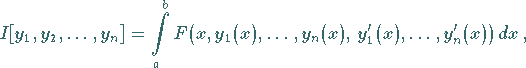
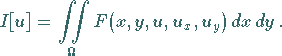
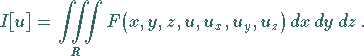
![]() im Integralausdruck der Variationsaufgabe nur die erste Ableitung
im Integralausdruck der Variationsaufgabe nur die erste Ableitung ![]() oder höhere Ableitungen
oder höhere Ableitungen ![]() der Funktion
der Funktion ![]() enthält.
enthält.
![]() hat dann z.B. der
Integralausdruck (10.2) die Form
hat dann z.B. der
Integralausdruck (10.2) die Form