Lineare Ausgleichsaufgaben
Gegeben sei das überbestimmte lineare Gleichungssystem
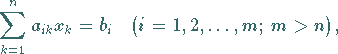 |
(19.37) |
in Matrixschreibweise
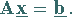 |
(19.38) |
Die Koeffizientenmatrix 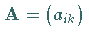 ,
die vom Typ
,
die vom Typ 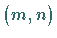 ist, habe den
Maximalrang
ist, habe den
Maximalrang 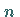 ,
d.h., ihre Spalten sind linear unabhängig.
Da ein überbestimmtes lineares Gleichungssystem in der Regel keine Lösung hat, geht
man von (19.37) zu den sogenannten Fehlergleichungen
,
d.h., ihre Spalten sind linear unabhängig.
Da ein überbestimmtes lineares Gleichungssystem in der Regel keine Lösung hat, geht
man von (19.37) zu den sogenannten Fehlergleichungen
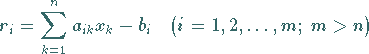 |
(19.39) |
mit den Residuen 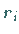 über und verlangt, daß die Summe der Quadrate der
Residuen minimal wird:
über und verlangt, daß die Summe der Quadrate der
Residuen minimal wird:
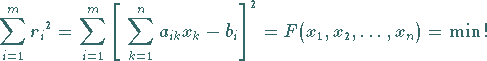 |
(19.40) |
Die Aufgabe (19.40) wird als lineare Ausgleichsaufgabe oder
lineares Quadratmittelproblem bezeichnet.
Die notwendigen Bedingungen dafür, daß die Fehlerquadratsumme
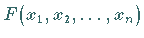 ein relatives Minimum annimmt, lauten
ein relatives Minimum annimmt, lauten
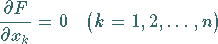 |
(19.41) |
und führen auf das lineare Gleichungssystem
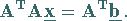 |
(19.42) |
Der Übergang von (19.38) zu (19.42) wird
als GAUSS-Transformation bezeichnet, da das System
(19.42) durch Anwendung der
GAUSSschen Fehlerquadratmethode
aus (19.38) entstanden ist.
Da für 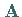 Maximalrang vorausgesetzt wurde, ist
Maximalrang vorausgesetzt wurde, ist  eine positiv definite Matrix vom Typ
eine positiv definite Matrix vom Typ 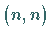 ,
und die sogenannten
Normalgleichungen (19.42) können mit Hilfe des
CHOLESKY-Verfahrens numerisch gelöst werden.
,
und die sogenannten
Normalgleichungen (19.42) können mit Hilfe des
CHOLESKY-Verfahrens numerisch gelöst werden.
Bei der Lösung des Normalgleichungssystems (19.42) können
numerische Probleme auftreten, wenn die Konditionszahl
(s. Lit. 19.27) der Matrix  sehr groß ist.
Die Lösung
sehr groß ist.
Die Lösung 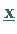 kann dann große relative Fehler haben.
Deshalb ist es numerisch günstiger, zur Lösung linearer Ausgleichsaufgaben
Orthogonalisierungsverfahren zu verwenden.
kann dann große relative Fehler haben.
Deshalb ist es numerisch günstiger, zur Lösung linearer Ausgleichsaufgaben
Orthogonalisierungsverfahren zu verwenden.
![]() sehr groß ist.
Die Lösung
sehr groß ist.
Die Lösung ![]() kann dann große relative Fehler haben.
Deshalb ist es numerisch günstiger, zur Lösung linearer Ausgleichsaufgaben
Orthogonalisierungsverfahren zu verwenden.
kann dann große relative Fehler haben.
Deshalb ist es numerisch günstiger, zur Lösung linearer Ausgleichsaufgaben
Orthogonalisierungsverfahren zu verwenden.