Definition der kubischen Interpolationssplines
Es seien 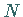 Interpolationspunkte
Interpolationspunkte 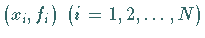 gegeben.
Der kubische Interpolationsspline
gegeben.
Der kubische Interpolationsspline 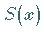 ist durch folgende Eigenschaften
eindeutig festgelegt:
ist durch folgende Eigenschaften
eindeutig festgelegt:
1. 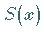 erfüllt die Interpolationsbedingung
erfüllt die Interpolationsbedingung
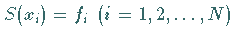 .
.
2. 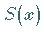 ist in jedem Teilintervall
ist in jedem Teilintervall
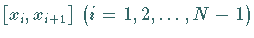 ein Polynom vom Grad
ein Polynom vom Grad 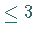 .
.
3. 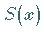 ist 2mal stetig differenzierbar im gesamten Approximationsintervall
ist 2mal stetig differenzierbar im gesamten Approximationsintervall
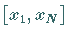 .
.
4. 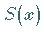 erfüllt spezielle Randbedingungen:
erfüllt spezielle Randbedingungen:
a) 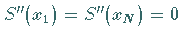 (man spricht dann von natürlichen Splines )
oder
(man spricht dann von natürlichen Splines )
oder
b) 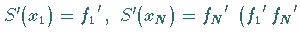 sind gegebene Werte) oder
sind gegebene Werte) oder
c) 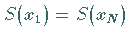 ,
falls
,
falls 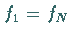 ,
und
,
und 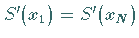 sowie
sowie
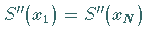 (man spricht dann von periodischen Splines ).
(man spricht dann von periodischen Splines ).
Aus diesen Eigenschaften folgt, daß 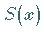 unter allen 2mal stetig differenzierbaren
Funktionen
unter allen 2mal stetig differenzierbaren
Funktionen 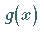 ,
die die Interpolationsbedingung
,
die die Interpolationsbedingung
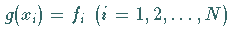 erfüllen, dadurch ausgezeichnet ist, daß
erfüllen, dadurch ausgezeichnet ist, daß
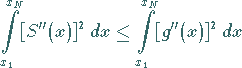 |
(19.230) |
gilt ( Satz von HOLLADAY ).
Man sagt auf Grund von (19.230), 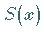 hat minimale Gesamtkrümmung ,
da für die Krümmung
hat minimale Gesamtkrümmung ,
da für die Krümmung 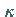 einer ebenen Kurve in erster Näherung
einer ebenen Kurve in erster Näherung
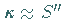 gilt (s. Abschnitt Krümmung und Krümmungskreis).
Darüber hinaus läßt sich zeigen:
Legt man durch die Punkte
gilt (s. Abschnitt Krümmung und Krümmungskreis).
Darüber hinaus läßt sich zeigen:
Legt man durch die Punkte 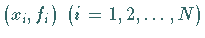 ein dünnes, elastisches
Lineal (engl. Spline), so wird seine Biegelinie durch den kubischen Interpolationsspline
ein dünnes, elastisches
Lineal (engl. Spline), so wird seine Biegelinie durch den kubischen Interpolationsspline
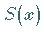 beschrieben.
beschrieben.