Zur numerischen Bestimmung von 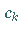 wendet man auf (19.218b)
analog zu (19.209) und (19.210) die
Trapezformel an und erhält die diskreten komplexen FOURIER-Koeffizienten
wendet man auf (19.218b)
analog zu (19.209) und (19.210) die
Trapezformel an und erhält die diskreten komplexen FOURIER-Koeffizienten
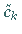 :
:
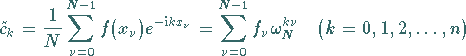 |
(19.221a) |
mit
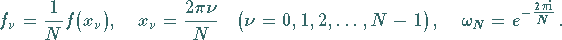 |
(19.221b) |
Der Zusammenhang (19.221a) unter Beachtung von (19.221b) wird dann als
diskrete komplexe FOURIER-Transformation der Länge 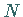 der Werte
der Werte
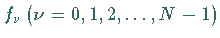 bezeichnet.
bezeichnet.
Die Potenzen 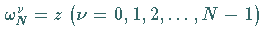 genügen sämtlich der
Gleichung
genügen sämtlich der
Gleichung 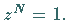 Sie werden deshalb auch als
Sie werden deshalb auch als 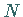 - te Einheitswurzel
bezeichnet. Wegen
- te Einheitswurzel
bezeichnet. Wegen  gilt:
gilt:
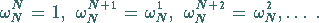 |
(19.222) |
Die effektive Berechnung der Summe (19.221a) ergibt sich aus der Tatsache, daß
eine diskrete komplexe FOURIER-Transformation der Länge  auf zwei
Transformationen der Länge
auf zwei
Transformationen der Länge 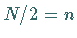 in folgender Weise zurückgeführt werden kann:
in folgender Weise zurückgeführt werden kann:
a) Für alle Koeffizienten
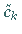 mit geradem Index,
d.h.
mit geradem Index,
d.h. 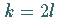 ,
erhält man:
,
erhält man:
Dabei wurde beachtet, daß
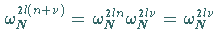 ist.
Substituiert man
ist.
Substituiert man
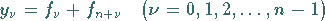 |
(19.223) |
und berücksichtigt man, daß 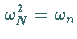 gilt, dann ist
gilt, dann ist
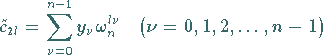 |
(19.224) |
die diskrete komplexe FOURIER-Transformation der Werte
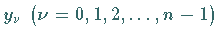 mit der Länge
mit der Länge 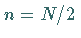 .
.
b) Für alle Koeffizienten
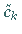 mit ungeradem
Index, d.h. mit
mit ungeradem
Index, d.h. mit 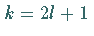 ,
erhält man analog:
,
erhält man analog:
Substituiert man
 |
(19.225) |
und beachtet man, daß auch hier 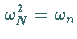 gilt, dann ist
gilt, dann ist
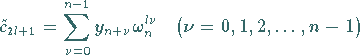 |
(19.226) |
die diskrete komplexe FOURIER-Transformation der Werte
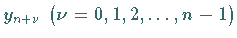 mit der Länge
mit der Länge 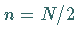 .
.
Die Reduzierung gemäß a) und b), d.h. die Zurückführung einer
diskreten komplexen FOURIER-Transformation auf jeweils zwei
diskrete komplexe FOURIER-Transformationen der halben Länge, läßt sich
fortsetzen, wenn 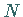 eine Potenz von 2 ist, d.h. wenn
eine Potenz von 2 ist, d.h. wenn  (
(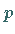 natürliche
Zahl) gilt.
Die
natürliche
Zahl) gilt.
Die 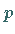 -malige Anwendung der Reduzierung wird als FFT bezeichnet.
Da jeder Reduktionsschritt wegen (19.225)
-malige Anwendung der Reduzierung wird als FFT bezeichnet.
Da jeder Reduktionsschritt wegen (19.225) 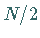 komplexe Multiplikationen erfordert,
ist der Rechenaufwand bei der FFT von der Größenordnung
komplexe Multiplikationen erfordert,
ist der Rechenaufwand bei der FFT von der Größenordnung
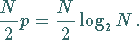 |
(19.227) |
![]() auf zwei
Transformationen der Länge
auf zwei
Transformationen der Länge ![]() in folgender Weise zurückgeführt werden kann:
in folgender Weise zurückgeführt werden kann:
![]() mit geradem Index,
d.h.
mit geradem Index,
d.h. ![]() ,
erhält man:
,
erhält man:
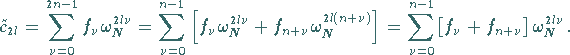
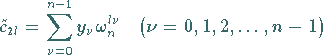
![]() mit der Länge
mit der Länge ![]() .
.
![]() mit ungeradem
Index, d.h. mit
mit ungeradem
Index, d.h. mit ![]() ,
erhält man analog:
,
erhält man analog:
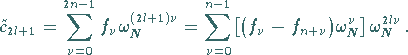
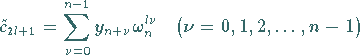
![]() mit der Länge
mit der Länge ![]() .
.
![]() eine Potenz von 2 ist, d.h. wenn
eine Potenz von 2 ist, d.h. wenn ![]() (
(![]() natürliche
Zahl) gilt.
Die
natürliche
Zahl) gilt.
Die ![]() -malige Anwendung der Reduzierung wird als FFT bezeichnet.
Da jeder Reduktionsschritt wegen (19.225)
-malige Anwendung der Reduzierung wird als FFT bezeichnet.
Da jeder Reduktionsschritt wegen (19.225) ![]() komplexe Multiplikationen erfordert,
ist der Rechenaufwand bei der FFT von der Größenordnung
komplexe Multiplikationen erfordert,
ist der Rechenaufwand bei der FFT von der Größenordnung