|
|
|
|
sollen die dazugehörigen 3 Reduktionsschritte
der FFT gemäß (19.223) und (19.225) im
folgenden Schema 1 zusammengestellt werden:
-Werten des
3. Schrittes erkennt man, wenn man sich überlegt, wie in jedem Reduktionsschritt jeweils
die Berechnung der Koeffizienten mit geraden und ungeraden Indizes erfolgt.
In dem folgenden Schema 2 ist diese Verfahrensweise schematisch dargestellt.
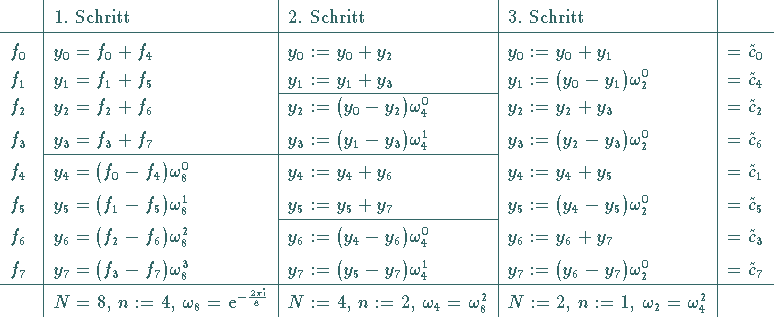
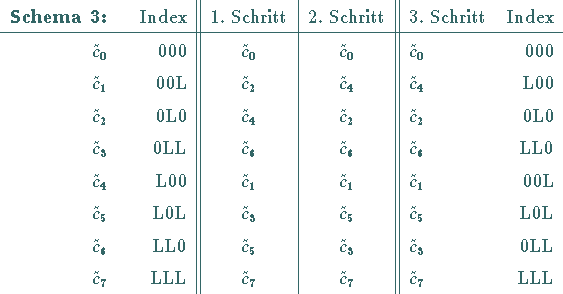
Schreibt man in Schema 1 die Koeffizienten 
auf und gibt man die
Dualdarstellung ihrer Indizes vor dem ersten und nach dem dritten Reduktionsschritt an,
dann erkennt man, daß die Reihenfolge der gesuchten Koeffizienten durch sogenannte
Bitumkehr
auf besonders einfache Weise ermittelt werden kann, wie in dem folgenden Schema 3
dargestellt ist.
| Beispiel | |||||||||||
|
Für die Funktion
Aus dem dritten (letzten) Reduktionsschritt erhält man die nachstehend aufgeführten gesuchten reellen FOURIER-Koeffizienten gemäß (19.220):
In diesem Beispiel kann man auch die allgemeine Eigenschaft | |||||||||||
 |
(19.229) |
sieht man, daß gilt:
.
|
|
,
die periodisch mit der
Periode 
sein soll,
werde mit Hilfe der FFT die diskrete FOURIER-Transformation durchgeführt.
Man wähle 
.
Mit
,
erhält man das folgende Schema 4:
