Sei 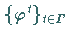 ein glattes dynamisches System auf
ein glattes dynamisches System auf 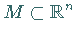 ,
das einen Attraktor
,
das einen Attraktor 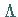 mit einem dort konzentrierten invarianten ergodischen
Wahrscheinlichkeitsmaß
mit einem dort konzentrierten invarianten ergodischen
Wahrscheinlichkeitsmaß 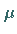 hat.
Für beliebige
hat.
Für beliebige 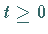 und
und 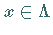 seien
seien
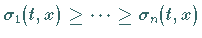 die Singulärwerte der JACOBI-Matrix
die Singulärwerte der JACOBI-Matrix
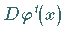 von
von 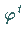 im Punkt
im Punkt 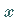 .
Dann existiert eine Folge von Zahlen
.
Dann existiert eine Folge von Zahlen 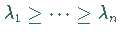 ( LYAPUNOV- Exponenten ), so daß
( LYAPUNOV- Exponenten ), so daß
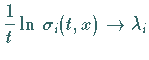 für
für
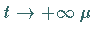 -fast überall im Sinne von
-fast überall im Sinne von 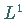 gilt.
gilt.
Satz von Oseledec: Nach dem Satz von OSELEDEC existiert 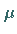 -fast
überall eine Folge von Teilräumen des
-fast
überall eine Folge von Teilräumen des 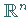
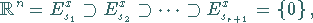 |
(17.38) |
so daß für 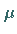 -fast alle
-fast alle 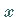 die Größe
die Größe
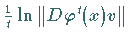 gleichmäßig bezüglich
gleichmäßig bezüglich
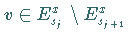 gegen ein Element
gegen ein Element
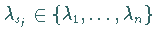 strebt.
strebt.
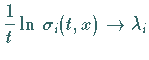 für
für
![]() -fast
überall eine Folge von Teilräumen des
-fast
überall eine Folge von Teilräumen des ![]()