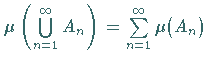Maß einer Funktion

Maß einer Funktion

Eine auf einer

-Algebra

definierte Funktion

heißt Maß, wenn
a)

impliziert

.
Die Eigenschaft c) heißt

- Additivität des Maßes. Ist

ein Maß auf

und sind

, dann ist

(Monotonie). Wenn

und

, dann

(Stetigkeit von unten).

Seien eine -Algebra von Teilmengen aus und ein Maß auf . Das Tripel heißt Maßraum , und die Mengen aus heißen meßbar oder - meßbar .

Beispiel A

Seien eine endliche Menge die -Algebra aller Teilmengen von , und sei jedem eine nichtnegative Zahl zugeordnet. Dann ist die für jede Menge durch auf definierte Funktion ein Maß, das (wegen nur endliche Werte annehmende sogenannte Zählmaß.

Beispiel B

DIRAC-Maß: Seien eine -Algebra von Teilmengen einer Menge und ein beliebig fixierter Punkt aus . Durch

ist auf ein Maß definiert. Es heißt (auf konzentrierte) - Funktion . Offensichtlich gilt (s. Stetige lineare Funktionale), wobei die charakteristische Funktion der Menge bezeichnet.

Beispiel C

LEBESGUE-Maß: Seien ein metrischer Raum und die kleinste -Algebra von Teilmengen aus , die alle offenen Mengen von enthält. existiert als der Durchschnitt aller -Algebren, die die Gesamtheit aller offenen Mengen enthalten, und heißt die BORELsche -Algebra von . Jedes Element aus heißt BOREL-Menge (s. Lit. 12.6). Sei jetzt . Mit Hilfe einer Erweiterungsprozedur kann man eine -Algebra und darauf ein Maß konstruieren, das auf der Menge aller Quader aus mit dem Volumen übereinstimmt. Genauer: Es existiert eine eindeutig bestimmte -Algebra von Teilmengen aus und ein eindeutig bestimmtes Maß auf mit den folgenden Eigenschaften:
a) Jede offene Menge aus gehört zu , mit anderen Worten: .
b) Aus und folgen und .
c) Ist ein Quader, dann ist , und es gilt .
d) ist translationsinvariant, d.h. für jeden Vektor und jede Menge gelten
und .
Die Elemente aus heißen LEBESGUE-meßbare Teilmengen von . ist das (-dimensionale) LEBESGUE-Maß in .

Hinweis: Man sagt in der Maß- und Integrationstheorie, daß eine Behauptung (Eigenschaft, Bedingung) bezüglich eines Maßes fast überall oder - fast überall auf einer Menge gilt, wenn die Menge, auf der sie nicht erfüllt ist, das Maß Null hat. Man schreibt dafür auch die Abkürzung f.ü. bzw. -f.ü. Also, ist etwa das LEBESGUE-Maß auf , sind zwei disjunkte Mengen mit und ist eine Funktion auf mit und , dann ist -f.ü. auf genau dann, wenn .

Beispiel A
	Seien eine endliche Menge die -Algebra aller Teilmengen von , und sei jedem eine nichtnegative Zahl zugeordnet. Dann ist die für jede Menge durch auf definierte Funktion ein Maß, das (wegen nur endliche Werte annehmende sogenannte Zählmaß.

Beispiel B
	DIRAC-Maß: Seien eine -Algebra von Teilmengen einer Menge und ein beliebig fixierter Punkt aus . Durch ist auf ein Maß definiert. Es heißt (auf konzentrierte) - Funktion . Offensichtlich gilt (s. Stetige lineare Funktionale), wobei die charakteristische Funktion der Menge bezeichnet.