|
|
|
|
| Beispiel A | |
|
Gegeben sei die Rotationsabbildung des Kreises mit | |
| Beispiel B | |
|
Dynamische Systeme mit stabilen Ruhelagen oder stabilen periodischen Orbits als
Attraktoren sind bezüglich des natürlichen Maßes ergodisch.
| |
Ergodensatz von Birkhoff:
Das dynamische System ![]() sei ergodisch bezüglich des
invarianten Wahrscheinlichkeitsmaßes
sei ergodisch bezüglich des
invarianten Wahrscheinlichkeitsmaßes ![]() .
Dann stimmen für jede integrierbare Funktion
.
Dann stimmen für jede integrierbare Funktion ![]() die
Zeitmittel entlang des positiven Semiorbits
die
Zeitmittel entlang des positiven Semiorbits ![]() ,
d.h.
,
d.h.
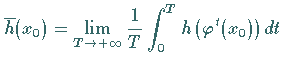 für Flüsse und
für Flüsse und
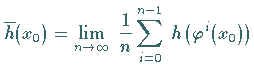 für diskrete Systeme, für
für diskrete Systeme, für ![]() -fast alle Punkte
-fast alle Punkte ![]() mit dem Raummittel
mit dem Raummittel
![]() überein.
überein.
|
|
|