Periodische Orbits
Sei 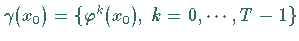 ein
ein 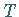 -periodischer Orbit
-periodischer Orbit
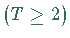 von (17.3).
Dann heißt
von (17.3).
Dann heißt 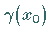 hyperbolisch , wenn
hyperbolisch , wenn 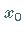 eine hyperbolische Ruhelage
der Abbildung
eine hyperbolische Ruhelage
der Abbildung 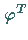 ist.
ist.
Die Matrix 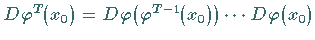 heißt Monodromie -Matrix; die Eigenwerte
heißt Monodromie -Matrix; die Eigenwerte 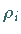 von
von 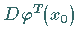 sind
die Multiplikatoren von
sind
die Multiplikatoren von 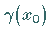 .
.
Sind alle Multiplikatoren 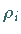 von
von 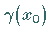 vom Betrag kleiner 1, so ist der
periodische Orbit
vom Betrag kleiner 1, so ist der
periodische Orbit 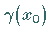 asymptotisch stabil.
asymptotisch stabil.
![]() von
von ![]() vom Betrag kleiner 1, so ist der
periodische Orbit
vom Betrag kleiner 1, so ist der
periodische Orbit ![]() asymptotisch stabil.
asymptotisch stabil.