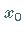|
|
|
|
eine Ruhelage von (17.3) mit 
.
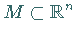Das lokale Verhalten der Iteration (17.3) nahe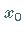
wird, unter
gewissen Voraussetzungen, durch die Variationsgleichung
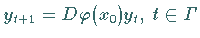bestimmt.
Besitzt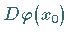 
keinen Eigenwert 
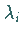mit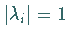 
,
so
heißt die Ruhelage 
,
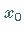analog zum Differentialgleichungfall,
hyperbolisch .
Die hyperbolische Ruhelage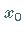
ist vom Typ 
,
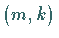wenn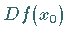 
genau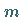 
Eigenwerte innerhalb und 
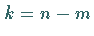Eigenwerte außerhalb des komplexen
Einheitskreises besitzt.
Die hyperbolische Ruhelage vom Typ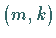 
heißt für 
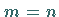Senke ,
für 
Quelle und für 
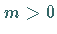und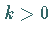 
Sattel .
Es gilt der folgende
Satz über Stabilität in der ersten Näherung für diskrete dynamische Systeme:
Eine Senke ist asymptotisch stabil; Quellen und Sattel sind instabil.
|
|