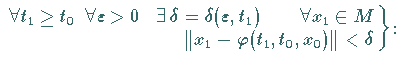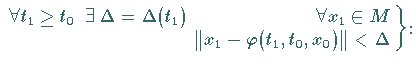|
Gegeben sei ein Fluß in 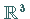 ,
der den Torus ,
der den Torus 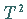 als invariante Menge besitzt.
Lokal sei in Winkelkoordinaten der Fluß beschrieben durch
als invariante Menge besitzt.
Lokal sei in Winkelkoordinaten der Fluß beschrieben durch
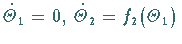 ,
wobei ,
wobei
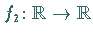 eine
eine 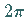 -periodische glatte Funktion sei, für die
gilt: -periodische glatte Funktion sei, für die
gilt:
Eine beliebige Lösung mit Anfang 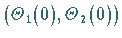 auf
dem Torus ist gegeben durch
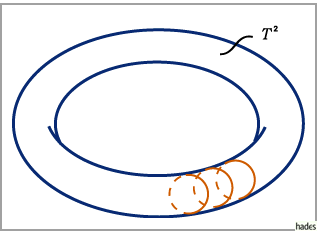
An dieser Darstellung erkennt man, daß jede Lösung orbital stabil ist, aber nicht
LYAPUNOV-stabil (s. Abbildung).
auf
dem Torus ist gegeben durch
An dieser Darstellung erkennt man, daß jede Lösung orbital stabil ist, aber nicht
LYAPUNOV-stabil (s. Abbildung).
|